题目内容
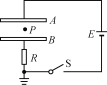
【题目】如图所示，上端带卡环的绝热圆柱形气缸竖直放置在水平地面上，气缸内部的高度为h，气缸内部被厚度不计、质量均为m的活塞A和B分成高度相等的三部分，下边两部分封闭有理想气体M和N，活塞A导热性能良好，活塞B绝热，两活塞均与气缸接触良好，不计一切摩擦，N部分气体内有加热装置，初始状态温度为T0，气缸的横截面积为S，外界大气压强大小为
且保持不变。现对N部分气体缓慢加热
（1）当活塞A恰好到达气缸上端卡环时，N部分气体从加热装置中吸收的热量为Q，求该过程中N部分气体内能的变化量；
（2）活塞A恰好接触气缸上端卡环后，继续给N部分气体加热，当M部分气体的高度达到
时，求此时N部分气体的温度。
【答案】(i)Q-mgh(ⅱ)
【解析】
(ⅰ)活塞A到达气缸上端卡环前，气体M和N均做等压变化，活塞A、B之间的距离不变。当活塞A恰好到达气缸上端卡环时，
N部分气体的压强pN2=pM1+
=p0+
=
①
N部分气体增加的体积ΔV=
②
N部分气体对外做功W=pN2·ΔV=mgh③
N部分气体内能的变化量ΔU=Q-W=Q-mgh④
(ⅱ)活塞A恰好接触气缸上端卡环后，继续给N部分气体加热，气体M做等温变化，由玻意耳定律
·
S=pM2·
S⑤
解得pM2=
⑥
此时N部分气体的压强pN3=pM2+=
⑦
N部分气体的体积VN3=
S⑧
对N部分气体由理想气体状态方程
=
⑨
解得
⑩
练习册系列答案
相关题目
