题目内容
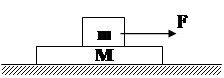
如图,光滑的水平面上有一质量为M=3 m的长板车A,其上放有一质量为m的滑块B(可看作质点),B的右端被一个固定在A车上的轻质挡栓C挡住(C与A车右端尚有一点长度可略的空隙).A车右端到竖直墙的距离是L0=2S,用一恒力F=4mg水平向右推B,使A、B一起向右匀加速运动,在A与墙发生碰撞前的瞬间去掉力F和挡栓,不计A车与墙、B与A车碰撞的能量损失.试求:

(1)A与墙碰撞前的瞬间的速度大小
(2)若车足够长,B不会从A的左端滑出,则AB一起向左匀速运动的速度多大
(3)若车长L=16 S,为了保证B不滑离A,B与A车间的摩擦因数μ应满足的关系
答案:
解析:
解析:
|
解:(1)(5分)以AB作为整体,设A墙碰前的速度为v0, 由动能定理得: 解得: (2)(5分)取向左的方向为正方向,由题意A与墙碰后瞬间的速度为为v0,此时B的速度为-v0,设A|、B最终的共同速度为v,A与墙碰后的整个过程动量守恒,故有: 解得: (3)(5分)因为A与B的碰撞无能量损失,则要使B不滑离A,必须:( 解得: 评分标准:①③⑤每式3分,②④⑥每式2分 写出: 解得结果 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
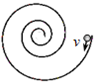 如图,光滑的水平面上固定着一个半径在逐渐减小的螺旋形光滑水平轨道.一个小球以一定速度沿轨道切线方向进入轨道,下列物理量中数值将减小的是( )
如图,光滑的水平面上固定着一个半径在逐渐减小的螺旋形光滑水平轨道.一个小球以一定速度沿轨道切线方向进入轨道,下列物理量中数值将减小的是( )| A、周期 | B、线速度 | C、角速度 | D、向心加速度 |
 每式给1分,
每式给1分, 如图,光滑的水平面上停放有一块长1.0m,质量为1.0kg的木板A,木板A的左端搁放一质量为2.0kg的小金属块B(B可视为质点),B与A之间的动摩擦因数μ=0.1,现对金属块施加一水平向右的外力F=10N,使A、B由静止开始运动.
如图,光滑的水平面上停放有一块长1.0m,质量为1.0kg的木板A,木板A的左端搁放一质量为2.0kg的小金属块B(B可视为质点),B与A之间的动摩擦因数μ=0.1,现对金属块施加一水平向右的外力F=10N,使A、B由静止开始运动.