题目内容
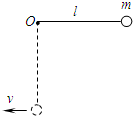 用一根长为l=0.8m的轻质不可伸长的细绳把一个质量为m=0.2kg的小球悬挂在点O,将小球拉至与悬点等高处由静止释放,如图所示(g取10m/s2).求:
用一根长为l=0.8m的轻质不可伸长的细绳把一个质量为m=0.2kg的小球悬挂在点O,将小球拉至与悬点等高处由静止释放,如图所示(g取10m/s2).求:(1)取小球摆动的最低点为重力势能的零点,小球在最高点的重力势能.
(2)小球经过最低点时的速度大小.
(3)小球经过最低点时,细绳的拉力F.
分析:(1)根据Ep=mgh求解重力势能;
(2)根据机械能守恒定律列式求解;
(3)拉力和重力的合力提供向心力,根据牛顿第二定律列式求解.
(2)根据机械能守恒定律列式求解;
(3)拉力和重力的合力提供向心力,根据牛顿第二定律列式求解.
解答:解:(1)取小球摆动的最低点为重力势能的零点,小球在最高点的重力势能:
Ep=mgl=0.2kg×10N/kg×0.8m=1.6J
(2)小球下摆过程中,只有重力做功,机械能守恒,故:
mgl=
mv2
解得:v=
=
=4m/s
(3)小球经过最低点时,拉力和重力的合力提供向心力,根据牛顿第二定律,有:
F-mg=m
F=mg+m
=0.2×10+0.2×
=6N
答:(1)取小球摆动的最低点为重力势能的零点,小球在最高点的重力势能为1.6J.
(2)小球经过最低点时的速度大小为4m/s.
(3)小球经过最低点时,细绳的拉力F为6N.
Ep=mgl=0.2kg×10N/kg×0.8m=1.6J
(2)小球下摆过程中,只有重力做功,机械能守恒,故:
mgl=
| 1 |
| 2 |
解得:v=
| 2gl |
| 2×10×0.8 |
(3)小球经过最低点时,拉力和重力的合力提供向心力,根据牛顿第二定律,有:
F-mg=m
| v2 |
| l |
F=mg+m
| v2 |
| l |
| 16 |
| 0.8 |
答:(1)取小球摆动的最低点为重力势能的零点,小球在最高点的重力势能为1.6J.
(2)小球经过最低点时的速度大小为4m/s.
(3)小球经过最低点时,细绳的拉力F为6N.
点评:本题关键是明确小球摆动过程中机械能守恒,能够根据守恒定律列式求解最低速度;在最低点,能够根据牛顿第二定律和向心力公式列式求解拉力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
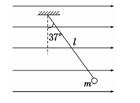
 用一根长为L的丝线吊着一质量为m、带电荷量为q的小球,小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.现突然将该电场方向变为向竖直上,但大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g,sin37°=0.6,cos37°=0.8),如图所示,求:
用一根长为L的丝线吊着一质量为m、带电荷量为q的小球,小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.现突然将该电场方向变为向竖直上,但大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g,sin37°=0.6,cos37°=0.8),如图所示,求: