题目内容
11. 如图所示,光滑斜面的倾角θ=30°,轻弹簧的劲度系数为k,两端分别与物体M和N相连,两物体的质量均为m,与斜面垂直的固定挡板P挡住N,两物体均处于静止状态.现沿平行斜面向下方向施加外力F压物体M,使得撤去外力F后,物体N能被弹簧拉起离开挡板(弹簧形变未超过其弹性限度),则外力F至少要做的功是( )
如图所示,光滑斜面的倾角θ=30°,轻弹簧的劲度系数为k,两端分别与物体M和N相连,两物体的质量均为m,与斜面垂直的固定挡板P挡住N,两物体均处于静止状态.现沿平行斜面向下方向施加外力F压物体M,使得撤去外力F后,物体N能被弹簧拉起离开挡板(弹簧形变未超过其弹性限度),则外力F至少要做的功是( )| A. | $\frac{{{m^2}{g^2}}}{2k}$ | B. | $\frac{{3{m^2}{g^2}}}{2k}$ | C. | $\frac{{2{m^2}{g^2}}}{k}$ | D. | $\frac{{5{m^2}{g^2}}}{2k}$ |
分析 物体N能被弹簧拉起离开挡板时,弹簧的弹力等于N的重力沿斜面向下的分力,由胡克定律求出开始与N刚离开挡板时弹簧的形变量,得到M上升的距离,抓住初末状态弹性势能相等,根据系统的机械能守恒列式求解.
解答 解:无F作用时,弹簧的弹力等于M的重力沿斜面向下的分力,则弹簧的压缩量为:x1=$\frac{mgsin30°}{k}$=$\frac{mg}{2k}$
物体N刚好被弹簧拉起离开挡板时,弹簧的弹力等于N的重力沿斜面向下的分力,则弹簧的伸长量为:x2=$\frac{mgsin30°}{k}$=$\frac{mg}{2k}$
由于x2=x1,所以物体N刚好被弹簧拉起离开挡板时,弹簧的弹性势能等于未加F时弹簧的弹性势能.对整个过程,根据能量守恒定律得:W=mgsin30°(x1+x2)=$\frac{{m}^{2}{g}^{2}}{2k}$
选项A正确,BCD错误
故选:A
点评 本题的关键理清初末状态,分析清楚弹簧的形变量关系,判断出初末状态的弹性势能相等.要知道物体相对于原位置上升的距离为x1+x2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.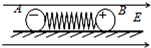 如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )
如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )
 如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )
如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )| A. | 因电场力分别对球A和球B做正功,故系统机械可能增加 | |
| B. | 因两个小球所受电场力等大反向,故系统机械能守恒 | |
| C. | 当弹簧长度达到最大值时,系统机械能最小 | |
| D. | 当小球所受电场力与弹簧的弹力相等时,系统动能最大 |
6. 如图,把塑料匙在干燥的布上摩擦几下,然后去舀爆米花,爆米花就会到处乱蹦.发生这种情况的原因是( )
如图,把塑料匙在干燥的布上摩擦几下,然后去舀爆米花,爆米花就会到处乱蹦.发生这种情况的原因是( )
 如图,把塑料匙在干燥的布上摩擦几下,然后去舀爆米花,爆米花就会到处乱蹦.发生这种情况的原因是( )
如图,把塑料匙在干燥的布上摩擦几下,然后去舀爆米花,爆米花就会到处乱蹦.发生这种情况的原因是( )| A. | 爆米花与带电的勺子接触,带同种电荷 | |
| B. | 爆米花与带电的勺子接触,带异种电荷 | |
| C. | 爆米花受到塑料匙的作用力而到处乱跳 | |
| D. | 爆米花是因为静电感应的带电,到外乱跳 |
16. 如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )
如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )
 如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )
如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )| A. | 一定是球先落在斜面上 | |
| B. | 可能是a球先落在半圆轨道上 | |
| C. | 当v0>$\frac{2\sqrt{10gR}}{5}$时,一定是a球先落到半圆轨道上 | |
| D. | 当v0<$\frac{4\sqrt{3gR}}{5}$时,一定是b球先落在斜面上 |
20.如图为物体做变速直线运动的v-t图象,令t=0时物体的位置为坐标原点,只研究前4s的运动,可知( )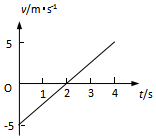
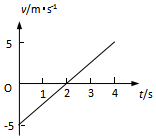
| A. | 物体始终沿正方向运动 | |
| B. | 物体先沿负方向运动,2s后开始沿正方向运动 | |
| C. | 在2s末物体回到坐标原点 | |
| D. | 在2s内物体的位移大小为5m |
1.下列说法中正确的是( )
| A. | 物体的加速度减小,其速度一定减小 | |
| B. | 物体的加速度越大,其速度变化越快 | |
| C. | 物体的加速度为零,其速度一定为零 | |
| D. | 物体的加速度越小,其速度变化越小 |
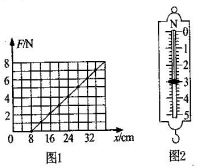 某同学在做“探究弹力和弹簧伸长的关系”实验时,通过处理数据得到了如图1所示的F-x图象,其中F为弹簧弹力,x为弹簧长度.
某同学在做“探究弹力和弹簧伸长的关系”实验时,通过处理数据得到了如图1所示的F-x图象,其中F为弹簧弹力,x为弹簧长度.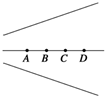 图为电场的电场线,现将一电荷量q=-3.0×10-9 C的负电荷从A点移到B点、从B点移到C点,从C点移到D点电场力做功分别为:WAB=3.0×10-8 J、WBC=1.5×10-8 J、WCD=9.0×10-9 J.若取C点电势为零,试求A、B、D三点电势.
图为电场的电场线,现将一电荷量q=-3.0×10-9 C的负电荷从A点移到B点、从B点移到C点,从C点移到D点电场力做功分别为:WAB=3.0×10-8 J、WBC=1.5×10-8 J、WCD=9.0×10-9 J.若取C点电势为零,试求A、B、D三点电势. 如图所示,小车的顶棚上用绳线吊一小球,质量为m,车厢底板上放一个质量为M的木块,当小车沿水平面匀加速向右运动时,小球悬线偏离竖直方向30°,木块和车厢保持相对静止,g取10m/s2,求:
如图所示,小车的顶棚上用绳线吊一小球,质量为m,车厢底板上放一个质量为M的木块,当小车沿水平面匀加速向右运动时,小球悬线偏离竖直方向30°,木块和车厢保持相对静止,g取10m/s2,求: