Question

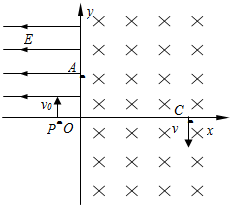
如图甲所示，一个质量为m，带电量为q的离子，从D点以某一初速度垂直进入匀强磁场．磁场方向垂直纸面向内，磁感应强度为B．正离子的初速度方向在纸面内，与直线AD的夹角为60°．结果粒子正好穿过AD的垂线上离A点距离为d的小孔C，垂直AC的方向进入AC右边的匀强电场中．电场的方向与AC平行．离子最后打在DA直线上的P点．P到A的距离为2d．不计重力，
求：（1）离子从D到P的运动时间；
（2）离子到达P点时的动能．

Answer 1

（1）画出粒子的运动轨迹如图．

由几何关系：R+Rsin30°=d
得：R=

2

3

d
由洛伦兹力提供向心力：qvB=

mv2

R

得：v=

2Bqd

3m

粒子在磁场中的运动周期：T=

2πR

v

=

2πm

qB

粒子在磁场中的运动的时间：t=

120°

360°

T=

2πm

3qB

粒子在电场中作类平抛运动：水平匀速，竖直匀加速
d=

1

2

at2=

1

2

vyt2
2d=vt₂
解得vy=v=

2Bqd

3m

t2=

2d

v

=

3m

qB

所以，粒子从D到P的时间为：t=t1+t2=

2πm

3qB

+

3m

qB

=

(2π+9)m

3qB

粒子到达P的动能：EK=

1

2

m(v2+

v

2y

)=mv2=

4B2q2d2

9m

答：：（1）离子从D到P的运动时间t=

(2π+9)m

3qB

；
（2）离子到达P点时的动能EK=

4B2q2d2

9m

．