题目内容
两根完全相同的金属裸导线，如果把其中一根均匀拉长到原来的两倍，把另一根对折后绞合起来，然后给它们分别加上相同的电压，则导线某一横截面上通过相同的电荷量所用的时间之比为（ ）A．1：8
B．8：1
C．1：16
D．16：1
【答案】分析：根据电阻定律R=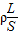
求出两根导线的电阻之比，再根据欧姆定律求出电流比，从而通过电流的定义式
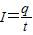求出通过相同的电荷量所用的时间之比．
解答：解：两根完全相同的金属裸导线，如果把其中一根均匀拉长到原来的两倍，把另一根对折后绞合起来，长度比为4：1，体积不变，则横截面积比1：4．根据电阻定律R=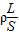
得，电阻比为16：1．
根据欧姆定律I=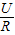
得，电流比为1：16．再根据
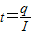得，时间比为16：1．故D正确，A、B、C错误．
故选D．
点评：解决本题的关键掌握电阻定律、欧姆定律以及电流的定义式．
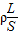求出两根导线的电阻之比，再根据欧姆定律求出电流比，从而通过电流的定义式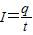求出通过相同的电荷量所用的时间之比．解答：解：两根完全相同的金属裸导线，如果把其中一根均匀拉长到原来的两倍，把另一根对折后绞合起来，长度比为4：1，体积不变，则横截面积比1：4．根据电阻定律R=
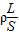得，电阻比为16：1．根据欧姆定律I=
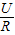得，电流比为1：16．再根据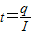得，时间比为16：1．故D正确，A、B、C错误．故选D．
点评：解决本题的关键掌握电阻定律、欧姆定律以及电流的定义式．
练习册系列答案
相关题目