题目内容
 如图所示,质量M的带有小孔的塑料块沿斜面向上滑动到达最高点C时的速度恰好为零,此时与从A点水平射出的弹丸相碰,弹丸沿着斜面方向进入塑料块中,并立即与塑料块具有相同的速度v=1m/s.已知A点和C点距地面的高度分别为H=1.95m,h=0.15m,弹丸的质量m,水平速度v0=8m/s,g=10m/s2.求:?
如图所示,质量M的带有小孔的塑料块沿斜面向上滑动到达最高点C时的速度恰好为零,此时与从A点水平射出的弹丸相碰,弹丸沿着斜面方向进入塑料块中,并立即与塑料块具有相同的速度v=1m/s.已知A点和C点距地面的高度分别为H=1.95m,h=0.15m,弹丸的质量m,水平速度v0=8m/s,g=10m/s2.求:?(1)斜面与水平面的夹角.(也可用反三角函数表示)
(2)若在斜面下端与地面交接处,设一个垂直斜面的弹性挡板,塑料块与它相碰没有机械能损失,斜面与塑料间的滑动摩擦系数为μ=0.25,则滑块从接收到弹丸至停止运动共通过多少路程?
分析:(1)弹丸A做平抛运动,到达C点时,弹丸沿着斜面方向进入塑料块中,说明其偏离初速度方向夹角与斜面倾角相等,恰为θ,利用运动的分解的方法可求出此角度.
(2)滑块从接收到弹丸后停止运动时,一定停在斜面的底端,对整体运用动能定理,即可求解路程.
(2)滑块从接收到弹丸后停止运动时,一定停在斜面的底端,对整体运用动能定理,即可求解路程.
解答:解:(1)解:(1)对弹丸从开始到C点过程,研究竖直方向的分运动,设到C点时竖直方向分速度为vy,根据运动学公式vy2=2g(H-h)
得 vy=6m/s所以此时弹丸速度方向偏离原方向的夹角θ满足:tanθ=
=
=
所以,θ=37°
依题意知,斜面与水平地面夹角也为θ=37°
(2)滑块最终会停止在斜面底端,设滑块从接收到弹丸至停止共走的路程为S,由动能定理得:
(M+m)gh-μ(M+m)gcosθS=0-
(M+m)v2
得:S=
=
m=1m.
答:(1)斜面与水平面的夹角为37°.
(2)滑块从接收到弹丸至停止运动共通过的路程为1m.
得 vy=6m/s所以此时弹丸速度方向偏离原方向的夹角θ满足:tanθ=
| vy |
| v0 |
| 6 |
| 8 |
| 3 |
| 4 |
所以,θ=37°
依题意知,斜面与水平地面夹角也为θ=37°
(2)滑块最终会停止在斜面底端,设滑块从接收到弹丸至停止共走的路程为S,由动能定理得:
(M+m)gh-μ(M+m)gcosθS=0-
| 1 |
| 2 |
得:S=
| 2gh+v2 |
| 2μgcosθ |
| 2×10×0.15+1 |
| 2×0.25×10×0.8 |
答:(1)斜面与水平面的夹角为37°.
(2)滑块从接收到弹丸至停止运动共通过的路程为1m.
点评:运动情况较复杂的题目,要注意分解过程,针对不同的过程应用规律求解,同时注意挖掘隐含条件,例如“恰好”“刚刚'“沿斜面方向”等

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
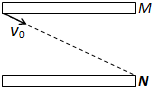 如图所示,水平放置的带电平行板电容器两极板M、N间距为d,质量为m、电荷量为q的带正电的粒子从上极板M的左边缘以初速度v0射入,沿直线从下极板N的右边缘射出,已知重力加速度为g,则下列说法中正确的是( )
如图所示,水平放置的带电平行板电容器两极板M、N间距为d,质量为m、电荷量为q的带正电的粒子从上极板M的左边缘以初速度v0射入,沿直线从下极板N的右边缘射出,已知重力加速度为g,则下列说法中正确的是( )| A、粒子的加速度不为零 | ||
B、两极板间电势差为
| ||
| C、M板电势低于N板电势 | ||
| D、粒子的机械能增加 |
 (2011?佛山二模)如图所示,质量m=0.015kg的木块Q放在水平桌面上的A点.A的左边光滑,右边粗糙,与木块间的动摩擦因数μ=0.08.在如图的两条虚线之间存在竖直向上的匀强电场和水平向里的匀强磁场,场强分别为E=20N/C、B=1T.场区的水平宽度d=0.2m,竖直方向足够高.带正电的小球P,质量M=0.03kg,电荷量q=0.015C,以v0=0.5m/s的初速度向Q运动.与Q发生正碰后,P在电、磁场中运动的总时间t=1.0s.不计P和Q的大小,P、Q碰撞时无电量交换,重力加速度g取10m/s2,计算时取π=3,试求:
(2011?佛山二模)如图所示,质量m=0.015kg的木块Q放在水平桌面上的A点.A的左边光滑,右边粗糙,与木块间的动摩擦因数μ=0.08.在如图的两条虚线之间存在竖直向上的匀强电场和水平向里的匀强磁场,场强分别为E=20N/C、B=1T.场区的水平宽度d=0.2m,竖直方向足够高.带正电的小球P,质量M=0.03kg,电荷量q=0.015C,以v0=0.5m/s的初速度向Q运动.与Q发生正碰后,P在电、磁场中运动的总时间t=1.0s.不计P和Q的大小,P、Q碰撞时无电量交换,重力加速度g取10m/s2,计算时取π=3,试求:
