题目内容
5. 如图,一个质量为m=2kg的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆管BCD的B点沿切线方向进入圆弧,经BCD从圆管的最高点D射出,恰好又落到B点.已知圆弧的半径为R=0.5m且A与D在同一水平线上,BC弧对应的圆心角θ=53°,不计空气阻力.求:
如图,一个质量为m=2kg的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆管BCD的B点沿切线方向进入圆弧,经BCD从圆管的最高点D射出,恰好又落到B点.已知圆弧的半径为R=0.5m且A与D在同一水平线上,BC弧对应的圆心角θ=53°,不计空气阻力.求:(1)小球从A点做平抛运动的初速度v0的大小;
(2)在D点处管壁对小球的作用力N的大小及其方向;
(3)小球在圆管中运动时克服阻力做的功Wf.
分析 (1)根据几何关系求出平抛运动下降的高度,从而求出竖直方向上的分速度,根据运动的合成和分解求出初速度的大小.
(2)根据平抛运动知识求出小球在D点的速度,再根据牛顿第二定律求出管壁对小球的弹力作用.
(3)对A到D全程运用动能定理,求出小球在圆管中运动时克服阻力做的功
解答 解:(1)小球从A到B:
竖直方向v${\;}_{y}^{2}$=2gR(1+cos53°)=3.2gR
则vy=$\sqrt{3.2×10×0.5}$=4m/s
在B点,由速度关系v0=$\frac{{v}_{y}}{tan53°}$=$\frac{4}{\frac{4}{3}}$m/s=3m/s
(2)小球从D到B:竖直方向R(1+cos53°)=$\frac{1}{2}$gt2
解得:t=$\sqrt{\frac{0.5×(1+0.6)×2}{10}}$s=0.4s
则小球从D点抛出的速度vD=$\frac{{Rsin{{53}^0}}}{t}$=$\frac{0.5×0.8}{0.4}$=1m/s
在D点,由向心力公式得:mg-N=m$\frac{{v}_{D}^{2}}{R}$
解得:N=2×10$-2×\frac{{1}^{2}}{0.5}$=16 N 方向竖直向上
(3)从A到D全程应用动能定理:-Wl=$\frac{1}{2}$mv${\;}_{D}^{2}$-$\frac{1}{2}$m${v}_{0}^{2}$
解得:Wl=$\frac{1}{2}×2$×32-$\frac{1}{2}×2$×12=8J
答:(1)小球从A点做平抛运动的初速度v0的大小为3m/s;
(2)在D点处管壁对小球的作用力N的大小为16N,其方向竖直向上;
(3)小球在圆管中运动时克服阻力做的功8J.
点评 本题综合考查了平抛运动和圆周运动的基础知识,难度不大,关键搞清平抛运动在水平方向和竖直方向上的运动规律,以及圆周运动向心力的来源.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图所示,电流表事先已经接好,拿电压表的K接线柱去分别试触b、c两点,电流表示数分别为0.04A和0.03A,电压表示数分别为2.9V和3V.则待测电阻的真实值应为( )
如图所示,电流表事先已经接好,拿电压表的K接线柱去分别试触b、c两点,电流表示数分别为0.04A和0.03A,电压表示数分别为2.9V和3V.则待测电阻的真实值应为( )| A. | 比100Ω略大一些 | B. | 比100Ω略小一些 | C. | 比72.5Ω略大一些 | D. | 比72.5Ω略小一些 |
| A. | $\frac{{a}_{1}+{a}_{2}}{2}$ | B. | $\frac{{m}_{1}{a}_{1}}{{m}_{1}+{m}_{2}}$ | C. | $\frac{{m}_{2}{a}_{2}}{{m}_{1}+{m}_{2}}$ | D. | $\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$ |
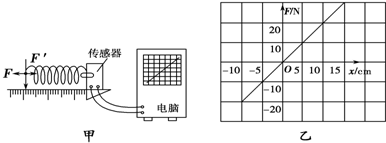
| A. | 弹簧产生的弹力和弹簧的长度成正比 | |
| B. | 弹簧长度的增加量与对应的弹力增加量成正比 | |
| C. | 该弹簧的劲度系数是200 N/m | |
| D. | 该弹簧受到反向压力时,劲度系数不变 |

| A. | a点电势比b点高 | |
| B. | a、b两点的场强方向相同,a点场强比b点大 | |
| C. | a、b、c三点和无穷远处等电势,且均为零 | |
| D. | 一个电子在a点的电势能比在b点的电势能大 |
 如图所示,在电场强度E=2.0×104N/C的匀强电场中,一带正电的点电荷在A点所受电场力F=2.0×10-4N.
如图所示,在电场强度E=2.0×104N/C的匀强电场中,一带正电的点电荷在A点所受电场力F=2.0×10-4N.  质量为m,带电量为-q的微粒(重力不计),经过匀强电场中的A点时速度为v,方向与电场线垂直,运动到B点时速度大小为2v,如下图所示.已知A、B两点间的距离为d.求:
质量为m,带电量为-q的微粒(重力不计),经过匀强电场中的A点时速度为v,方向与电场线垂直,运动到B点时速度大小为2v,如下图所示.已知A、B两点间的距离为d.求: