题目内容
如图轨道是由一直轨道和一半圆轨道组成，一个小滑块从距轨道最低点B为h的A处由静止开始运动，滑块质量为m，不计一切摩擦．则（ ）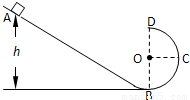
A．若滑块能通过圆轨道最高点D，h最小为2.5R
B．若h=2R，当滑块到达与圆心等高的C点时，对轨道的压力为3mg
C．若h=2R，滑块会从C、D之间的某个位置离开圆轨道做斜抛运动
D．若要使滑块能返回到A点，则h≤R
【答案】分析：物体进入右侧半圆轨道后做圆周运动，由圆周运动的临界条件可知物体能到达D点的临界值；再由机械能守恒定律可得出A点最小高度，分情况讨论即可．
解答：解：A、要使物体能通过最高点，则由mg=m
可得：v=
，从A到D根据机械能守恒定律得：mgh=mg2R+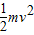
，解得h=2.5R，故A正确；
B、若h=2R，从A到C根据机械能守恒定律得：mgh=mgR+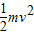
，在C点有：N=m
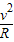，解得：N=2mg，故B错误；
C、若h=2R，小滑块不能通过D点，在CD中间某一位置即做斜上抛运动离开轨道，做斜抛运动，故C正确；
D、若要使滑块能返回到A点，则物块在圆弧中运动的高度不能超过C点，否则就不能回到A点，则则h≤R，故D正确．
故选ACD
点评：机械能守恒定律与圆周运动的结合题目较为常见，在解题时一定要把握好竖直平面内圆周运动的临界值的分析．
解答：解：A、要使物体能通过最高点，则由mg=m
可得：v=，从A到D根据机械能守恒定律得：mgh=mg2R+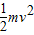，解得h=2.5R，故A正确；B、若h=2R，从A到C根据机械能守恒定律得：mgh=mgR+
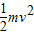，在C点有：N=m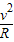，解得：N=2mg，故B错误；C、若h=2R，小滑块不能通过D点，在CD中间某一位置即做斜上抛运动离开轨道，做斜抛运动，故C正确；
D、若要使滑块能返回到A点，则物块在圆弧中运动的高度不能超过C点，否则就不能回到A点，则则h≤R，故D正确．
故选ACD
点评：机械能守恒定律与圆周运动的结合题目较为常见，在解题时一定要把握好竖直平面内圆周运动的临界值的分析．
练习册系列答案
初中学业考试导与练系列答案
相关题目
如图轨道是由一直轨道和一半圆轨道组成，一个小滑块从距轨道最低点B为h的A处由静止开始运动，滑块质量为m，不计一切摩擦．则（ ）
