题目内容
 如图所示,ABC为一绝缘轨道,其中AB段是位于竖直平面的
如图所示,ABC为一绝缘轨道,其中AB段是位于竖直平面的| 1 | 4 |
(1)小物块到达B点时速度的大小.
(2)小物块进入水平轨道BC后,受到电场力和支持力的大小各是多少?
(3)小物块进入水平轨道BC滑行,若经t=1.0s停下,则小物块与BC间的动摩擦因数为多少?
分析:(1)A到B的过程中只有重力做功,机械能守恒,根据机械能守恒定律求出小物块到达B点的速度大小.
(2)根据电场强度求出电场力的大小,根据竖直方向上平衡求出支持力的大小.
(3)根据速度时间公式求出匀减速直线运动的加速度,根据牛顿第二定律求出摩擦力的大小,结合f=μN求出动摩擦因数的大小.
(2)根据电场强度求出电场力的大小,根据竖直方向上平衡求出支持力的大小.
(3)根据速度时间公式求出匀减速直线运动的加速度,根据牛顿第二定律求出摩擦力的大小,结合f=μN求出动摩擦因数的大小.
解答:解:(1)小物块从A滑到B的过程,由机械能守恒定律得:mgR=
mvB2
解得:vB=
=
m/s=3m/s
(2)小物块在BC轨道上受到的电场力的大小:
F电=qE=5.0×10-6×4.0×104 N=0.2N
小物块受到支持力的大小:
N=mg+F电=(0.1×l0+0.2)N=1.2N
(3)小物块在BC轨道上运动受力如图所示,做匀减速直线运动的加速度:
a=
=
=-3m/s2
根据牛顿第二定律得:f=ma=0.1×3N=-0.3 N
负号表示摩擦力方向与小物块运动方向相反.
所以,小物块与BC间的动摩擦因数为:
μ=
=
=0.25

答:(1)小物块到达B点时速度的大小为3m/s.
(2)小物块进入水平轨道BC后,受到电场力和支持力的大小分别为0.2N、1.2N.
(3)小物块与BC间的动摩擦因数为0.25.
| 1 |
| 2 |
解得:vB=
| 2gR |
| 2×10×0.45 |
(2)小物块在BC轨道上受到的电场力的大小:
F电=qE=5.0×10-6×4.0×104 N=0.2N
小物块受到支持力的大小:
N=mg+F电=(0.1×l0+0.2)N=1.2N
(3)小物块在BC轨道上运动受力如图所示,做匀减速直线运动的加速度:
a=
| 0-vB |
| t |
| -3 |
| 1 |
根据牛顿第二定律得:f=ma=0.1×3N=-0.3 N
负号表示摩擦力方向与小物块运动方向相反.
所以,小物块与BC间的动摩擦因数为:
μ=
| f |
| N |
| 0.3 |
| 1.2 |

答:(1)小物块到达B点时速度的大小为3m/s.
(2)小物块进入水平轨道BC后,受到电场力和支持力的大小分别为0.2N、1.2N.
(3)小物块与BC间的动摩擦因数为0.25.
点评:本题考查了机械能守恒定律,牛顿第二定律和运动学公式,难度不大,关键理清物体在整个过程中的运动规律,正确地进行受力分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
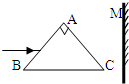 如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )
如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )| A、BC面将有色光射出 | B、光屏M上会出现色彩光带且紫光在上 | C、光屏M上会出现色彩光带且红光在上 | D、将光屏保持与BC垂直向右平移,屏上彩色光带宽度不变 |
 如图所示,ABC为一等腰直角玻璃棱镜的横截面,该玻璃临界角小于45°,一束白光平行于BC面射到AB面上,折射后能射到BC面上;该光束射出棱镜的情况是( )
如图所示,ABC为一等腰直角玻璃棱镜的横截面,该玻璃临界角小于45°,一束白光平行于BC面射到AB面上,折射后能射到BC面上;该光束射出棱镜的情况是( )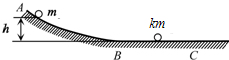 如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接.质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上.
如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接.质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上.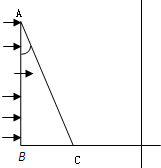 如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为
如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为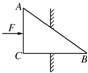 如图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜边AB=10cm,直角边AC=2cm.当用F=100N的力沿水平方向推劈时,求劈的AB面和BC面产生的推力各为多大?
如图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜边AB=10cm,直角边AC=2cm.当用F=100N的力沿水平方向推劈时,求劈的AB面和BC面产生的推力各为多大?