题目内容
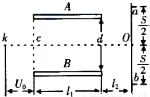
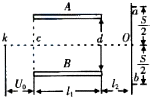 如图为示波器的部分构造,真空室中电极连续不断地发射电子(初速度不计),经过电压为Ua的加速电场后,由小孔C沿水平金属板A、B间的中心轴线射入两板间,板长为l1两板间距为d,电子穿过两板后,打在荧光屏上,屏到两板边缘的距离为l2,A,B两板间不加电压时,电子打在宽敞光屏的中点O上,屏上a、b两点到O点的距离均为
如图为示波器的部分构造,真空室中电极连续不断地发射电子(初速度不计),经过电压为Ua的加速电场后,由小孔C沿水平金属板A、B间的中心轴线射入两板间,板长为l1两板间距为d,电子穿过两板后,打在荧光屏上,屏到两板边缘的距离为l2,A,B两板间不加电压时,电子打在宽敞光屏的中点O上,屏上a、b两点到O点的距离均为| S | 2 |
(1)求出AB两板间所加电压的最大值;
(2)写出加在AB两板间电压U与时间t(0≤t≤T)的关系式;
(3)画出U-t图象.
分析:(1)电子经加速电场加速,进入偏转电场,做类平抛运动,出电场做匀速直线运动,根据运动学公式结合电子从偏转电场射出,不论U多大,电子都好像从偏转电场的中心O′射出,通过几何关系求出偏转电压与最终偏移量的关系.
(2)求t=0进入两板间的电子打在屏上的b点,然后在时间T内亮点匀速上移到a点,求出电子在屏上的偏移量与时间的关系,从而结合第(1)问中的结论求出U与时间的关系.
(3)根据U与t的关系式作出U-t图象.
(2)求t=0进入两板间的电子打在屏上的b点,然后在时间T内亮点匀速上移到a点,求出电子在屏上的偏移量与时间的关系,从而结合第(1)问中的结论求出U与时间的关系.
(3)根据U与t的关系式作出U-t图象.
解答:解:(1)设电子经Ua加速后的速度为v0,根据动能定理得:eUa=
mv02①
设电子偏转飞出电场与水平方向的夹角为θ
tanθ=
=
.②
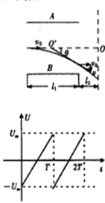
电子从偏转电场射出,不论U多大,电子都好像从偏转电场的中心O′射出.
如图,由几何关系得:
tanθ=
③
联立①②③解得y=
U④
所以U=
.
当y=
时,U有最大值,Umax=
.
(2)t时刻,亮点的位置y=
t-
由(1)式结论有:U(t)=
(
-
).
(3)如图所示.
答:(1)AB两板间所加电压的最大值为Umax=
.
(2)加在AB两板间电压U与时间t(0≤t≤T)的关系式为U(t)=
(
-
)
(3)如图所示.
| 1 |
| 2 |
设电子偏转飞出电场与水平方向的夹角为θ
tanθ=
| vy |
| v0 |
| eUl1 |
| dmv02 |
电子从偏转电场射出,不论U多大,电子都好像从偏转电场的中心O′射出.
如图,由几何关系得:
tanθ=
| y | ||
l2+
|
联立①②③解得y=
| (2l2+l1)l1 |
| 4Uad |
所以U=
| 4Uady |
| (2l2+l1)l1 |

当y=
| s |
| 2 |
| 2Uads |
| (2l2+l1) |
(2)t时刻,亮点的位置y=
| s |
| T |
| s |
| 2 |
由(1)式结论有:U(t)=
| 4Uads |
| (2l2+l1) |
| t |
| T |
| 1 |
| 2 |
(3)如图所示.
答:(1)AB两板间所加电压的最大值为Umax=
| 2Uads |
| (2l2+l1) |
(2)加在AB两板间电压U与时间t(0≤t≤T)的关系式为U(t)=
| 4Uads |
| (2l2+l1) |
| t |
| T |
| 1 |
| 2 |
(3)如图所示.
点评:解决本题的关键理清电子在整个过程中的运动情况,运用运动学公式结合牛顿第二定律求出偏移量,通过偏移量与偏转电压的关系,得出U与t的关系式.

练习册系列答案
相关题目

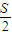 ,若在A、B两板间加上变化的电压,在每个电子通过极板的极短时间内,电场强度可视为恒定不变,现要求t=0进入两板间的电子打在屏上的b点,然后在时间T内亮点匀速上移到a点,在屏上形成一条竖直亮线,亮点到a点后又立即跳回到b点,以后不断重复这一过程,设电子的电荷量为e,质量为m.
,若在A、B两板间加上变化的电压,在每个电子通过极板的极短时间内,电场强度可视为恒定不变,现要求t=0进入两板间的电子打在屏上的b点,然后在时间T内亮点匀速上移到a点,在屏上形成一条竖直亮线,亮点到a点后又立即跳回到b点,以后不断重复这一过程,设电子的电荷量为e,质量为m.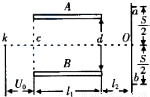
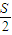 ,若在A、B两板间加上变化的电压,在每个电子通过极板的极短时间内,电场强度可视为恒定不变,现要求t=0进入两板间的电子打在屏上的b点,然后在时间T内亮点匀速上移到a点,在屏上形成一条竖直亮线,亮点到a点后又立即跳回到b点,以后不断重复这一过程,设电子的电荷量为e,质量为m.
,若在A、B两板间加上变化的电压,在每个电子通过极板的极短时间内,电场强度可视为恒定不变,现要求t=0进入两板间的电子打在屏上的b点,然后在时间T内亮点匀速上移到a点,在屏上形成一条竖直亮线,亮点到a点后又立即跳回到b点,以后不断重复这一过程,设电子的电荷量为e,质量为m.