��Ŀ����
һ������Ϊm������Ϊ+q��С����ˮƽ���ٶ�v0��h�߶���ƽ���˶������ƿ����������������ٶ�Ϊg���Իش��������⣺
��1�����ڿռ���ֱ�����һ����ǿ�糡������С��ˮƽ�׳���������ֱ���˶����糡ǿ��E�Ƕ��
��2��������ǿ�糡��С����ˮƽ�׳�����һ��ص�P�Ĺ��̣�����λ��S![]() �Ĵ�С�Ƕ��٣�
�Ĵ�С�Ƕ��٣�
��3�����ڿռ��ټ�һ����ֱֽ���������ǿ�ų�������С���һ�������Ȼ��P�㣬���ʴŸ�Ӧǿ��B�Ƕ��
��1��![]()
��2��
��3��![]()
����:
��1��mg=qE ![]() (2��)
(2��)
��2��![]() (1��)
(1��) ![]() (1��)
(1��)
�õ� (1��)
(1��)

��3��R2=x2+��R-h��2 (1��) ��![]() (1��)
(1��)
![]()
![]() (2��)
(2��)

��ϰ��ϵ�д�
�����Ŀ
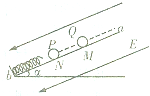 ��ͼ��ʾ�����Ϊa�Ĺ⻬б���¶˹̶�һ��Ե�ᵯ�ɣ�M��̶�һ������Ϊm��������Ϊ-q��С��Q������װ�ô��ڵ糡ǿ�ȴ�СΪE��������б�����µ���ǿ�糡�У��ְ�һ��������Ϊ+q��С��P��N���ɾ�ֹ�ͷţ��ͷź�P����б�������˶���N���뵯�ɵ��϶˺�M�ľ����Ϊs0��P��Q�Լ����ɵ�����ab��б��ƽ�У���С�������Ϊ�ʵ�͵��ɣ����ɵľ���ϵ��Ϊk0������������Ϊk��������
��ͼ��ʾ�����Ϊa�Ĺ⻬б���¶˹̶�һ��Ե�ᵯ�ɣ�M��̶�һ������Ϊm��������Ϊ-q��С��Q������װ�ô��ڵ糡ǿ�ȴ�СΪE��������б�����µ���ǿ�糡�У��ְ�һ��������Ϊ+q��С��P��N���ɾ�ֹ�ͷţ��ͷź�P����б�������˶���N���뵯�ɵ��϶˺�M�ľ����Ϊs0��P��Q�Լ����ɵ�����ab��б��ƽ�У���С�������Ϊ�ʵ�͵��ɣ����ɵľ���ϵ��Ϊk0������������Ϊk��������| A��С��P����ʱ������ײ��С��Q | ||||
B��С��P��N��ļ��ٶȴ�СΪ
| ||||
| C��С��P����б�������˶������У�������ܿ������� | ||||
D�������ɵ�ѹ����Ϊ
|
 ��2008?��ģ�⣩һ������Ϊm������Ϊ+q��С����ˮƽ���ٶ�v0�������h�߶ȴ���ƽ���˶������ƿ����������������ٶ�Ϊg���Իش��������⣺
��2008?��ģ�⣩һ������Ϊm������Ϊ+q��С����ˮƽ���ٶ�v0�������h�߶ȴ���ƽ���˶������ƿ����������������ٶ�Ϊg���Իش��������⣺ ��2009?ʯ��ɽ����ģ����ͼ��ʾ���ڴֲڡ���Ե���㹻���ˮƽ���Ϲ̶���һ��������ĵ���Q����һ������Ϊm������Ϊq��С�����飨����Ϊ�ʵ㣩����ˮƽ���ϲ��ɾ�ֹ�ͷţ������齫��ˮƽ������Զ��Q�ķ���ʼ�˶�����ˮƽ���㹻�����ڽ������˶��������������У�������
��2009?ʯ��ɽ����ģ����ͼ��ʾ���ڴֲڡ���Ե���㹻���ˮƽ���Ϲ̶���һ��������ĵ���Q����һ������Ϊm������Ϊq��С�����飨����Ϊ�ʵ㣩����ˮƽ���ϲ��ɾ�ֹ�ͷţ������齫��ˮƽ������Զ��Q�ķ���ʼ�˶�����ˮƽ���㹻�����ڽ������˶��������������У�������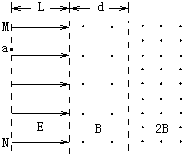 ��ͼ��ʾ��ˮƽ�������ǿ�糡�ij�ǿΪE���糡������ΪL����ֱ�����㹻���������ŵ糡���Ǵ�ֱֽ�������������ǿ�ų�������Ÿ�Ӧǿ�ȷֱ�ΪB��2B��һ������Ϊm������Ϊq�Ĵ���������ӣ������������ӵ糡�ı߽�MN�ϵ�a���ɾ�ֹ�ͷţ����糡���ٺ����ų�������tB=��m/4qB ʱ�䴩���м�ų��������ұߴų���Ȼ��ijһ·���ٷ��ص��糡�ı߽�MN�ϵ�ijһ��b������Ϊ�����ķֽ��棩����
��ͼ��ʾ��ˮƽ�������ǿ�糡�ij�ǿΪE���糡������ΪL����ֱ�����㹻���������ŵ糡���Ǵ�ֱֽ�������������ǿ�ų�������Ÿ�Ӧǿ�ȷֱ�ΪB��2B��һ������Ϊm������Ϊq�Ĵ���������ӣ������������ӵ糡�ı߽�MN�ϵ�a���ɾ�ֹ�ͷţ����糡���ٺ����ų�������tB=��m/4qB ʱ�䴩���м�ų��������ұߴų���Ȼ��ijһ·���ٷ��ص��糡�ı߽�MN�ϵ�ijһ��b������Ϊ�����ķֽ��棩����