题目内容
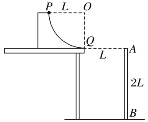
【题目】如图所示，一块质量为M=0.8kg、长为L的木板B放在光滑水平桌面上，B的左端有一质量为m＝0.2kg的物块A(可视为质点)，A上连接一根很长的轻质细绳，细绳跨过位于桌面边缘的定滑轮挂上一质量为m0＝0.1kg的重物，用手托住重物使细绳伸直但无张力，重物距离地面的高度为h＝1m。已知A与B之间的动摩擦因数μ＝0.2，A与滑轮间的细绳与桌面平行，B右端距离桌边定滑轮足够远。释放重物后，A相对于B滑动，取重力加速度g＝10m/s2。求：
(1)重物落地前瞬间细绳上的拉力大小和A的速度大小
(2)当A、B相对静止时，A仍在B上，求从释放重物到A、B相对静止的过程中，A、B运动的时间和系统由于摩擦而产生的热量。
【答案】(1) 0.8N；2m/s(2) 1.6s；0.48J
【解析】
(1)设释放重物后重物的加速度为a1，细绳的张力为FT，牛顿第二定律，对重物和A组成的系统有
m0g-
mg＝(m0+m)a1
解得
a1＝2m/s2
对A有
FT-mg＝ma1
解得
FT＝0.8N
对重物有
＝2a1h
解得
v1＝2m/s
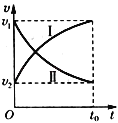
(2)重物落地前，A运动的时间
t1= 
=1s
B的加速度
重物落地时B的速度
v2＝a2t1＝0.5m/s
重物落地后，A、B系统水平方向动量守恒，设它们相对静止时的共同速度为v有
mv1+Mv2＝(m+M)v
解得
v＝0.8m/s
从释放重物到A、B相对静止的时间
t＝
=1.6s
A、B的相对位移
xA-xB＝h+ 
＝1.2m
根据功能关系可知系统由于摩擦而产生的热量
Q=umg(xA -xB)=0.48 J
练习册系列答案
相关题目
