题目内容
在倾角为θ的长斜面上有一带有风帆的滑块从静止开始沿斜面下滑，滑块质量为m，它与斜面间动摩擦因数为μ．帆受到的空气阻力与滑块下滑的速度大小成正比，即Ff=kv．?
（1）写出滑块下滑加速度的表达式．?
（2）写出滑块下滑的最大速度表达式．?
（3）若m=2kg，θ=30°，g取10m/s2．滑块从静止下滑的速度图象如图所示，图中直线是t=0时v-t图线的切线，由此求出μ、k的值．?
解：（1）对物体受力分析，受重力G、支持力FN、风力F风和滑动摩擦力F滑；
根据牛顿第二定律，有
Gsinθ-μGcosθ-kv=ma?
则：a=g（sinθ-μcosθ）-
v?
（2）当a=0时，v最大，
此时有：?Gsinθ=μGcosθ+kv最大?
则：v最大=
（3）由图象中直线部分可得：a=g（sinθ-μcosθ）=3 m/s2?
解得：μ=0.23
由图象曲线部分可得：?v最大=
=2 m/s?
解得：k=3.0?
答：（1）滑块下滑加速度的表达式为a=g（sinθ-μcosθ）-v；?
（2）滑块下滑的最大速度表达式为v最大=；?
（3）动摩擦因素的值为0.23，比例系数k为3.0．
分析：（1）对滑块进行受力分析，根据牛顿第二定律求出滑块下滑速度为v时加速度的表达式；
（2）根据第一问中得到加速度a与v的关系，当a=0时，v最大，写出滑块下滑的最大速度的表达式．
（3）图中直线是t=0时刻速度图线的切线，v-t图象中斜率代表加速度；根据速度图线最终滑块做匀速运动，根据平衡条件列出等求解．
点评：本题解题的关键在于正确进行受力分析，同时能正确理解图象的意义，根据物体的运动状态，则可由共点力的平衡条件求解．
根据牛顿第二定律，有
Gsinθ-μGcosθ-kv=ma?
则：a=g（sinθ-μcosθ）-
v?（2）当a=0时，v最大，
此时有：?Gsinθ=μGcosθ+kv最大?
则：v最大=
（3）由图象中直线部分可得：a=g（sinθ-μcosθ）=3 m/s2?
解得：μ=0.23
由图象曲线部分可得：?v最大=
=2 m/s?解得：k=3.0?
答：（1）滑块下滑加速度的表达式为a=g（sinθ-μcosθ）-
v；?（2）滑块下滑的最大速度表达式为v最大=
；?（3）动摩擦因素的值为0.23，比例系数k为3.0．
分析：（1）对滑块进行受力分析，根据牛顿第二定律求出滑块下滑速度为v时加速度的表达式；
（2）根据第一问中得到加速度a与v的关系，当a=0时，v最大，写出滑块下滑的最大速度的表达式．
（3）图中直线是t=0时刻速度图线的切线，v-t图象中斜率代表加速度；根据速度图线最终滑块做匀速运动，根据平衡条件列出等求解．
点评：本题解题的关键在于正确进行受力分析，同时能正确理解图象的意义，根据物体的运动状态，则可由共点力的平衡条件求解．
练习册系列答案
相关题目
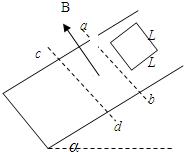如图所示，在倾角为a的光滑斜面上，abcd区域存在着垂直斜面向上的匀强磁场，边界ab和cd都沿水平方向，ac=L，在斜面上质量为m，边长为L的正方形导线框沿斜面自由下滑，恰好匀速穿过磁场，下列说法正确的是（ ）
如图所示，在倾角为37°的固定斜面上，有一个质量为5kg的物体静止放在斜面上，物体与斜面间的动摩擦因数μ为0.8．g取10m/s2，sin37°=0.6，cos37°=0.8，求：
如图所示，在倾角为θ=37°的固定斜面上，跨过定滑轮的轻绳一端系在小车的前端，另一端被坐在小车上的人拉住．已知人的质量为50kg，小车的质量为10kg，绳及滑轮的质量、滑轮与绳间的摩擦均不计，斜面对小车间的动摩擦因数为0.2，小车与人间的动摩擦因数为0.8，取重力加速度g=10m/s2，当人以288N的力拉绳时，人与小车相对静止，试求（斜面足够长）：（已知cos37°=0.8，sin37°=0.6．取g=10m/s2）
如图所示，有两根长为L、质量为m的细导体棒a、b，a被水平放置在倾角为45°的光滑斜面上，b被水平固定在与a在同一水平面的另一位置，且a、b平行，它们之间的距离为x，当两细棒中均通以电流强度为I的同向电流时，a恰能在斜面上保持静止，则下列关于b的电流在a处产生的磁场的磁感应强度的说法正确的是（ ）| A、方向向上 | ||||
B、大小为
| ||||
| C、要使a仍能保持静止，而减小b在a处的磁感应强度，可使b上移 | ||||
| D、若使b下移，a将不能保持静止 |
（2011?保定模拟）如图所示：在倾角为30°的光滑斜面上，底端固定着一垂直斜面的挡板p．斜面上有一长L=0.75m的木板A，木板的下端距挡板s=0.1m，木板的上端静止放着一小滑块B，木板和滑块的质量相等，滑块与木板的动摩擦因数μ=tan30°，由静止释放木板，当木板与挡板相撞时，不计机械能损失，且碰撞时间极短，g取10m/s2．求从木板A释放到滑块B滑出木板时的过程中所用时间．