题目内容
高空遥感探测卫星在距地球表面高为h处绕地球转动,如果地球质量为M,地球半径为R,人造卫星质量为m,万有引力常量为G,求:(1)人造卫星的角速度多大?
(2)人造卫星绕地球转动的周期是多少?
(3)人造卫星的向心加速度多大?
【答案】分析:(1)根据万有引力提供向心力G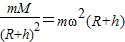 ,求出人造卫星的角速度.
,求出人造卫星的角速度.
(2)根据万有引力提供向心力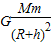 =m(R+h)
=m(R+h)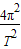 ,求出人造卫星的周期.
,求出人造卫星的周期.
(3)根据万有引力提供向心力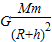 =ma,求出人造卫星的向心加速度.
=ma,求出人造卫星的向心加速度.
解答:解:(1)设卫星的角速度为ω,根据万有引力定律和牛顿第二定律有:
G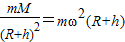 ,解得卫星线速度
,解得卫星线速度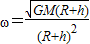
故人造卫星的角速度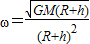 .
.
(2)由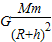 =m(R+h)
=m(R+h)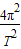 得周期T=
得周期T=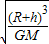 ?2π=2π(R+h)
?2π=2π(R+h)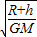
故人造卫星绕地球运行的周期为2π(R+h)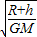 .
.
(3)由于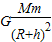 =m a可解得,向心加速度a=
=m a可解得,向心加速度a=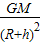
故人造卫星的向心加速度为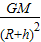 .
.
点评:解决本题的关键知道人造卫星绕地球运行靠万有引力提供向心力,即G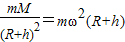 =m(R+h)
=m(R+h)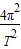 =ma.
=ma.
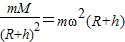 ,求出人造卫星的角速度.
,求出人造卫星的角速度.(2)根据万有引力提供向心力
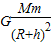 =m(R+h)
=m(R+h)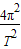 ,求出人造卫星的周期.
,求出人造卫星的周期.(3)根据万有引力提供向心力
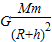 =ma,求出人造卫星的向心加速度.
=ma,求出人造卫星的向心加速度.解答:解:(1)设卫星的角速度为ω,根据万有引力定律和牛顿第二定律有:
G
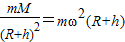 ,解得卫星线速度
,解得卫星线速度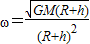
故人造卫星的角速度
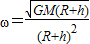 .
.(2)由
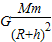 =m(R+h)
=m(R+h)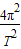 得周期T=
得周期T=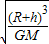 ?2π=2π(R+h)
?2π=2π(R+h)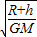
故人造卫星绕地球运行的周期为2π(R+h)
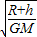 .
.(3)由于
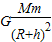 =m a可解得,向心加速度a=
=m a可解得,向心加速度a=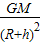
故人造卫星的向心加速度为
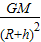 .
.点评:解决本题的关键知道人造卫星绕地球运行靠万有引力提供向心力,即G
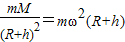 =m(R+h)
=m(R+h)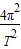 =ma.
=ma. 
练习册系列答案
相关题目