题目内容
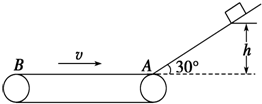 如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6m/s的速度运动,运动方向如图所示.一个质量为2kg的物体(物体可以视为质点),从h=3.2m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,g=10m/s2,则:
如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6m/s的速度运动,运动方向如图所示.一个质量为2kg的物体(物体可以视为质点),从h=3.2m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,g=10m/s2,则:(1)物体由静止沿斜面下滑到斜面末端的速度大小?
(2)为使物体不掉下传送带,传送带左右两端AB间的距离L至少为多少?
(3)物体在传送带上先向左运动后向右运动,最后沿斜面上滑所能达到的最大高度h′为多少?
分析:(1)物体由光滑斜面下滑的过程,只有重力做功,根据机械能守恒求解物体到斜面末端的速度大小.
(2)当物体滑到传送带最左端速度为零时,AB间的距离L最小,根据动能定理列式求解.
(3)物体在到达A点前速度与传送带相等,最后以v带=6m/s的速度冲上斜面时沿斜面上滑达到的高度最大,根据动能定理求解即可.
(2)当物体滑到传送带最左端速度为零时,AB间的距离L最小,根据动能定理列式求解.
(3)物体在到达A点前速度与传送带相等,最后以v带=6m/s的速度冲上斜面时沿斜面上滑达到的高度最大,根据动能定理求解即可.
解答:解:(1)物体由光滑斜面下滑的过程,只有重力做功,机械能守恒,则得:
mgh=
mv2
解得:v=
=
m/s=8m/s
(2)当物体滑到传送带最左端速度为零时,AB间的距离L最小,由动能定理得:
-μmgL=0-
mv2
解得:L=
=
m=6.4m
(3)物体在到达A点前速度与传送带相等,最后以v带=6m/s的速度冲上斜面,则根据动能定理得:
由 0-
mv带2=0-mgh′
得:h′=
=
m=1.8 m.
答:
(1)物体由静止沿斜面下滑到斜面末端的速度大小为8m/s.
(2)为使物体不掉下传送带,传送带左右两端AB间的距离L至少为6.4m.
(3)物体在传送带上先向左运动后向右运动,最后沿斜面上滑所能达到的最大高度h′为1.8m.
mgh=
| 1 |
| 2 |
解得:v=
| 2gh |
| 2×10×3.2 |
(2)当物体滑到传送带最左端速度为零时,AB间的距离L最小,由动能定理得:
-μmgL=0-
| 1 |
| 2 |
解得:L=
| v2 |
| 2μg |
| 82 |
| 2×0.5×10 |
(3)物体在到达A点前速度与传送带相等,最后以v带=6m/s的速度冲上斜面,则根据动能定理得:
由 0-
| 1 |
| 2 |
得:h′=
| ||
| 2g |
| 62 |
| 2×10 |
答:
(1)物体由静止沿斜面下滑到斜面末端的速度大小为8m/s.
(2)为使物体不掉下传送带,传送带左右两端AB间的距离L至少为6.4m.
(3)物体在传送带上先向左运动后向右运动,最后沿斜面上滑所能达到的最大高度h′为1.8m.
点评:该题要认真分析物体的受力情况和运动情况,选择恰当的过程,运用机械能守恒和动能定理解题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 如图所示,倾角为30°的光滑斜面静止在水平地面上,斜面上放一质量为2kg的小球,球被垂直于斜面的固定挡板挡住而处于静止状态,g取10m/s2.
如图所示,倾角为30°的光滑斜面静止在水平地面上,斜面上放一质量为2kg的小球,球被垂直于斜面的固定挡板挡住而处于静止状态,g取10m/s2. 如图所示,倾角为30°的斜面体固定在水平地面上,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的滑轮O(可视为质点).A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中B始终保持静止.则在绳子到达竖直位置之前,下列说法正确的是( )
如图所示,倾角为30°的斜面体固定在水平地面上,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的滑轮O(可视为质点).A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中B始终保持静止.则在绳子到达竖直位置之前,下列说法正确的是( ) 如图所示,倾角为θ=30°的斜面固定于水平地面上,在斜面底端0处固定有一轻弹簧,斜面顶端足够高.斜面上OM段光滑,M点的以上均粗糙.质量为m的物块A在M点恰好能静止,在离M点的距离为L的N点处,有一质量为2m的光滑物块B以速度V0=
如图所示,倾角为θ=30°的斜面固定于水平地面上,在斜面底端0处固定有一轻弹簧,斜面顶端足够高.斜面上OM段光滑,M点的以上均粗糙.质量为m的物块A在M点恰好能静止,在离M点的距离为L的N点处,有一质量为2m的光滑物块B以速度V0= (2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )
(2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( ) (2009?盐城一模)如图所示,倾角为30°的光滑斜面,底端固定一沿斜面方向的弹簧.一质量为m的滑块将弹簧压缩到A点(滑块与弹簧不连接),此时弹簧的压缩量为△L.滑块在A点由静止释放,沿斜面滑过距离L时速度为0.求:
(2009?盐城一模)如图所示,倾角为30°的光滑斜面,底端固定一沿斜面方向的弹簧.一质量为m的滑块将弹簧压缩到A点(滑块与弹簧不连接),此时弹簧的压缩量为△L.滑块在A点由静止释放,沿斜面滑过距离L时速度为0.求: