题目内容
 如图所示,质量m=0.015kg的木块Q放在水平桌面上的A点.A的左边光滑,右边粗糙,与木块间的动摩擦因数μ=0.08.在如图的两条虚线之间存在竖直向上的匀强电场和水平向里的匀强磁场,场强分别为E=20N/C、B=1T.场区的水平宽度d=0.2m,竖直方向足够高.带正电的小球P,质量M=0.03kg,电荷量q=0.015C,以v=0.5m/s的初速度向Q运动.与Q发生正碰后,P在电、磁场中运动的总时间t=1.0s.不计P和Q的大小,P、Q碰撞时无电量交换,重力加速度g取10m/s2,计算时取π=3,试求:
如图所示,质量m=0.015kg的木块Q放在水平桌面上的A点.A的左边光滑,右边粗糙,与木块间的动摩擦因数μ=0.08.在如图的两条虚线之间存在竖直向上的匀强电场和水平向里的匀强磁场,场强分别为E=20N/C、B=1T.场区的水平宽度d=0.2m,竖直方向足够高.带正电的小球P,质量M=0.03kg,电荷量q=0.015C,以v=0.5m/s的初速度向Q运动.与Q发生正碰后,P在电、磁场中运动的总时间t=1.0s.不计P和Q的大小,P、Q碰撞时无电量交换,重力加速度g取10m/s2,计算时取π=3,试求:(1)通过受力分析判断碰后P球在电、磁场中做什么性质的运动;
(2)P从电、磁场中出来时的速度大小;
(3)P从电、磁场中出来的时刻,Q所处的位置.
【答案】分析:P在电场中受电场力和磁场力以及重力作用,由题目给出的数据知,P受的重力和电场力平衡,P在复合场中的运动相当于只受洛伦兹力作用,故P做匀速圆周运动;P在磁场中运动时间为1s,已知磁场宽度,根据给出的数据可以求得P做圆周运动的同期,根据线速度的定义可以求出P在场中运动的速度V,因为P在场中做匀速圆周运动的速度即为P碰撞后的速度,所以根据动量守恒可以求得Q在碰撞后的速度,碰撞后Q在场中在摩擦力作用下做匀减速直线运动,故可以求出P从场中出来时Q的位移.
解答:解:P进入电、磁场后,受电场力、重力、洛伦兹力三力作用
电场力F=qE=0.3N
重力G=mg=0.3N
可见电场力与重力大小相等方向相反,两力平衡.
故相当于P在电、磁场中只受洛仑兹力作用,做匀速圆周运动;
(2)P在磁场中受洛伦兹力提供P作圆周运动的向心力
故有
得P做圆周运动的半径R= ①
①
周期
代入数据得T=12s
由已知条件,有
故如下图所示:
P的轨迹圆心角θ=30°

由右图可知,轨迹半径R=
结合①式得v=0.2m/s
(3)P和Q碰撞时,系统动量守恒,有
mv=mv+mQvQ
代入数据可解得vQ=0.6m/s
碰撞后Q水平方向只受摩擦力作用,应用牛顿第二定律,有
μmg=ma
得a=0.8m/s2
因为Q在摩擦力作用下做匀减速直线运动,取速度为正方向,故加速度a=-0.8m/s2
则Q停下前运动时间
由于t′<t,说明P离开电、磁场时,Q已经停下
故位移 =
=
即Q停留在右方距初始位置0.225m处.
答:(1)通过受力分析判断碰后P球在电、磁场中做匀速圆周运动;
(2)P从电、磁场中出来时的速度v=0.2m/s;
(3)P从电、磁场中出来的时刻,Q停留在右方距初始位置0.225m处.
点评:能根据粒子运动画出粒子运动的轨迹,并能根据轨迹求出粒子运动半径和已经量的关系,熟悉洛伦兹力提供向心力做匀速圆周运动半径、线速度、周期之间的关系.
解答:解:P进入电、磁场后,受电场力、重力、洛伦兹力三力作用
电场力F=qE=0.3N
重力G=mg=0.3N
可见电场力与重力大小相等方向相反,两力平衡.
故相当于P在电、磁场中只受洛仑兹力作用,做匀速圆周运动;
(2)P在磁场中受洛伦兹力提供P作圆周运动的向心力
故有

得P做圆周运动的半径R=
 ①
①周期

代入数据得T=12s
由已知条件,有

故如下图所示:
P的轨迹圆心角θ=30°

由右图可知,轨迹半径R=

结合①式得v=0.2m/s
(3)P和Q碰撞时,系统动量守恒,有
mv=mv+mQvQ
代入数据可解得vQ=0.6m/s
碰撞后Q水平方向只受摩擦力作用,应用牛顿第二定律,有
μmg=ma
得a=0.8m/s2
因为Q在摩擦力作用下做匀减速直线运动,取速度为正方向,故加速度a=-0.8m/s2
则Q停下前运动时间

由于t′<t,说明P离开电、磁场时,Q已经停下
故位移
 =
=
即Q停留在右方距初始位置0.225m处.
答:(1)通过受力分析判断碰后P球在电、磁场中做匀速圆周运动;
(2)P从电、磁场中出来时的速度v=0.2m/s;
(3)P从电、磁场中出来的时刻,Q停留在右方距初始位置0.225m处.
点评:能根据粒子运动画出粒子运动的轨迹,并能根据轨迹求出粒子运动半径和已经量的关系,熟悉洛伦兹力提供向心力做匀速圆周运动半径、线速度、周期之间的关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
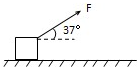 (2011?河南二模)如图所示,质量m=0.78kg的金属块放在水平桌面上,在斜向上的恒定拉力F作用下,向右以v0=2.0m/s的速度作匀速直线运动,已知F=3.0N,方向与水平面之间的夹角θ=37°.(sinθ=0.6,cosθ=0.8,g取10m/s2)
(2011?河南二模)如图所示,质量m=0.78kg的金属块放在水平桌面上,在斜向上的恒定拉力F作用下,向右以v0=2.0m/s的速度作匀速直线运动,已知F=3.0N,方向与水平面之间的夹角θ=37°.(sinθ=0.6,cosθ=0.8,g取10m/s2) 如图所示,质量M=0.2kg的足够长的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(相对地面)的过程中运动的路程.(可以认为长板与地面间的最大静摩擦力等于滑动摩擦力,g取10m/s2)
如图所示,质量M=0.2kg的足够长的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(相对地面)的过程中运动的路程.(可以认为长板与地面间的最大静摩擦力等于滑动摩擦力,g取10m/s2)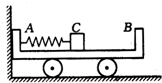 如图所示,质量M=0.8kg的小车静止在光滑的水平面上,左端紧靠竖直墙.在车上左端水平固定着一只弹簧,弹簧右端放一个质量m=0.2kg的滑块,弹簧为原长时,滑块位于C处(滑块可以视为质点),车的上表面AC部分为光滑水平面,CB部分为粗糙水平面.CB长l=1m、与滑块的摩擦因数μ=0.4.水平向左推动滑块,将弹簧压缩,然后再把滑块从静止释放,在压缩弹簧过程中推力做功2.5J,滑块释放后将在车上往复运动,最终停在车上某处.设滑块与车的B端碰撞时机械能无
如图所示,质量M=0.8kg的小车静止在光滑的水平面上,左端紧靠竖直墙.在车上左端水平固定着一只弹簧,弹簧右端放一个质量m=0.2kg的滑块,弹簧为原长时,滑块位于C处(滑块可以视为质点),车的上表面AC部分为光滑水平面,CB部分为粗糙水平面.CB长l=1m、与滑块的摩擦因数μ=0.4.水平向左推动滑块,将弹簧压缩,然后再把滑块从静止释放,在压缩弹簧过程中推力做功2.5J,滑块释放后将在车上往复运动,最终停在车上某处.设滑块与车的B端碰撞时机械能无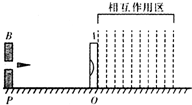 如图所示:质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分所示,当靶盒A进入相互作用区时便受指向O点的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒并每次发射一颗水平速度υ0=50m/s、质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.现约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.
如图所示:质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分所示,当靶盒A进入相互作用区时便受指向O点的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒并每次发射一颗水平速度υ0=50m/s、质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.现约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.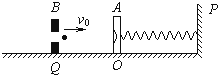 如图所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接,Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求
如图所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接,Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求