题目内容
1.在高速公路的拐弯处,路面往往设计成外高内低,设拐弯路段是半径为R的圆弧,要使车速为v时,车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,路面与水平面的夹角θ应等于多少?分析 车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零时,由重力与支持力的合力完全提供向心力,由牛顿第二定律列方程求解.
解答 解:据题车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,说明重力与支持力的合力完全提供向心力,重力、支持力的合力为:F=mgtanθ
根据牛顿第二定律得:mgtanθ=m$\frac{{v}^{2}}{R}$
解得:tanθ=$\frac{{v}^{2}}{gR}$
所以:θ=arctan$\frac{{v}^{2}}{gR}$
答:路面与水平面的夹角θ应等于arctan$\frac{{v}^{2}}{gR}$.
点评 该题是一个实际问题,考查了圆周运动向心力公式,要求同学们能够正确对物体进行受力分析,运用向心力知识解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左端,沿与水平方向成45°角的斜面向右上以速度v匀速运动,运动中始终保持悬线竖直,则橡皮的速度大小为 ( )
如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左端,沿与水平方向成45°角的斜面向右上以速度v匀速运动,运动中始终保持悬线竖直,则橡皮的速度大小为 ( )
 如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左端,沿与水平方向成45°角的斜面向右上以速度v匀速运动,运动中始终保持悬线竖直,则橡皮的速度大小为 ( )
如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左端,沿与水平方向成45°角的斜面向右上以速度v匀速运动,运动中始终保持悬线竖直,则橡皮的速度大小为 ( )| A. | $\sqrt{2}v$ | B. | $\frac{\sqrt{2}}{2}$v | C. | 2$\sqrt{2}$v | D. | $\sqrt{2+\sqrt{2}}v$ |
6. 单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )
单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )
 单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )
单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )| A. | 若磁场消失,仅有电场,则小球周期T>2π$\sqrt{\frac{l}{g}}$ | |
| B. | 若无电场,仅有磁场,且能保证小球正常摆动,则T>2π$\sqrt{\frac{l}{g}}$ | |
| C. | 单摆振动过程中机械能守恒 | |
| D. | 小球向右运动经过最低点时,绳的拉力最大 |
5. 如图所示M为理想变压器,电源电压不变,当变阻器的滑动头P向上移动时,各表的示数中肯定变小的是( )
如图所示M为理想变压器,电源电压不变,当变阻器的滑动头P向上移动时,各表的示数中肯定变小的是( )
 如图所示M为理想变压器,电源电压不变,当变阻器的滑动头P向上移动时,各表的示数中肯定变小的是( )
如图所示M为理想变压器,电源电压不变,当变阻器的滑动头P向上移动时,各表的示数中肯定变小的是( )| A. | A1 | B. | A2 | C. | V1 | D. | V2 |
2. 如图所示,一圆形闭合铜环由高处从静止开始下落,穿过一根竖直悬挂的条形磁铁(质量为m),铜环的中心轴线与条形磁铁的中轴始终保持重合.则悬挂磁铁的绳子中拉力F随时间t变化的图象可能是( )
如图所示,一圆形闭合铜环由高处从静止开始下落,穿过一根竖直悬挂的条形磁铁(质量为m),铜环的中心轴线与条形磁铁的中轴始终保持重合.则悬挂磁铁的绳子中拉力F随时间t变化的图象可能是( )
 如图所示,一圆形闭合铜环由高处从静止开始下落,穿过一根竖直悬挂的条形磁铁(质量为m),铜环的中心轴线与条形磁铁的中轴始终保持重合.则悬挂磁铁的绳子中拉力F随时间t变化的图象可能是( )
如图所示,一圆形闭合铜环由高处从静止开始下落,穿过一根竖直悬挂的条形磁铁(质量为m),铜环的中心轴线与条形磁铁的中轴始终保持重合.则悬挂磁铁的绳子中拉力F随时间t变化的图象可能是( )| A. |  | B. |  | C. |  | D. |  |
3. 如图所示,圆形区域内有垂直于纸面的匀强磁场,三个带电粒子a、b、c以相同速率对准圆心O沿AO方向射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力作用,则下列说法正确的是( )
如图所示,圆形区域内有垂直于纸面的匀强磁场,三个带电粒子a、b、c以相同速率对准圆心O沿AO方向射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力作用,则下列说法正确的是( )
 如图所示,圆形区域内有垂直于纸面的匀强磁场,三个带电粒子a、b、c以相同速率对准圆心O沿AO方向射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力作用,则下列说法正确的是( )
如图所示,圆形区域内有垂直于纸面的匀强磁场,三个带电粒子a、b、c以相同速率对准圆心O沿AO方向射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力作用,则下列说法正确的是( )| A. | a粒子动能最大 | B. | c粒子动能最大 | ||
| C. | b粒子在磁场中运动时间最长 | D. | 它们做圆周运动的周期Tc>Tb>Ta |
 如图所示这是一种自动跳闸的闸刀开关,O是固定轴,A是手柄,C是闸刀卡口,M,N是通电电极,磁场垂直纸面向里,磁感应强度为1T,CO间的距离是10cm,C处的最大摩擦力是1N,闸刀通电,电流经NOCM,当流过闸刀的电流为10A时,闸刀C处受的静摩擦力为1N,要使闸刀能自动跳闸,电流至少要达到10A.
如图所示这是一种自动跳闸的闸刀开关,O是固定轴,A是手柄,C是闸刀卡口,M,N是通电电极,磁场垂直纸面向里,磁感应强度为1T,CO间的距离是10cm,C处的最大摩擦力是1N,闸刀通电,电流经NOCM,当流过闸刀的电流为10A时,闸刀C处受的静摩擦力为1N,要使闸刀能自动跳闸,电流至少要达到10A.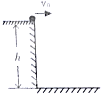 如图,平台高h=5m,小球以v0=10m/s的速度水平抛出,忽略空气阻力,求小球:
如图,平台高h=5m,小球以v0=10m/s的速度水平抛出,忽略空气阻力,求小球: 已知金属丝的电阻约为5Ω,现有如下器材:
已知金属丝的电阻约为5Ω,现有如下器材: