题目内容
如图所示，跨在光滑圆柱体侧面上的轻绳两端分别系有质量为mA、mB的小球，系统处于静止状态．A、B小球与圆心的连线分别与水平面成60°和30°角，则两球的质量之比和剪断轻绳时两球的加速度之比分别为（ ）A．
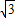：1 1：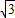
B．1：1 1：
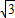
C．
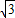：1 1：1D．1：1 1：2
【答案】分析：小球A、B分别受重力、支持力和绳子的拉力处于平衡，根据共点力平衡求出绳子拉力和重力的关系，抓住拉力相等，求出两球的质量比，剪断细线时，两球所受的合力与绳子的拉力等值反向，根据牛顿第二定律求出两球的加速度之比．
解答：解：两球受绳子的拉力F相等
受力分析得：F=mAgcos60°，F=mBgcos30°
所以mA：mB=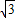
：1．
剪断细绳时，小球A、小球B所受的合力与绳子的拉力等值反向，根据牛顿第二定律得，
aA=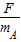
，aB=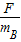
aA：aB=1：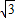
故选A．
点评：本题是简单的连接体问题，关键是受力分析，抓住绳子拉力相等，运用共点力平衡进行求解．
解答：解：两球受绳子的拉力F相等
受力分析得：F=mAgcos60°，F=mBgcos30°
所以mA：mB=
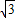：1．剪断细绳时，小球A、小球B所受的合力与绳子的拉力等值反向，根据牛顿第二定律得，
aA=
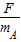，aB=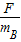aA：aB=1：
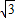
故选A．
点评：本题是简单的连接体问题，关键是受力分析，抓住绳子拉力相等，运用共点力平衡进行求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2005?徐汇区模拟）如图所示，一个碗口为圆弧形的半球形碗放在桌面上，O点为其球心，碗的内表面及碗口是光滑的，一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于静止状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°，则小球m1受到碗对它的支持力大小为
