题目内容
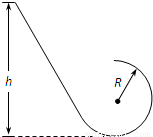
一质量m=2kg的小球从光滑斜面上高h=3.5m处由静止滑下，斜面底端紧接着一个半径R=1m的光滑圆环，如图所示，试求：（g=10m/s2）（1）小球滑至圆环顶点时对环的压力；
（2）小球至少应从多高处由静止滑下才能越过圆环最高点；
（3）小球从h'=2m处由静止滑下时，脱离圆环的位置和圆心的连线与竖直方向夹角的余弦．
【答案】分析：（1）小球在运动的过程中只有重力做功，机械能守恒，运用机械能守恒定律求出小球滑至圆环顶点时的速度，再根据牛顿第二定律求出轨道对球的弹力．
（2）小球通过最高点的临界情况是弹力为零，根据重力提供向心力求出最高点的临界速度，再根据机械能守恒定律求出小球初位置的高度．
（3）由于h'＜h1，故球在还没有到达顶端前即与环脱离，脱离的瞬间，重力沿半径方向上的合力提供向心力，结合牛顿第二定律和机械能守恒定律求出脱离圆环的位置和圆心的连线与竖直方向夹角的余弦．
解答：解：（1）设小球滑至环顶时的速度为υ1，所受环的压力为N．
小球运动过程中机械能守恒：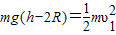
①
在顶点由圆周运动的知识有：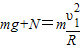
②
联立①②解得：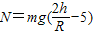
（
代入数值解得：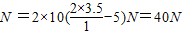
由牛顿第三定律知小球对环的压力大小为：N'=N=40N
（2）当圆环对小球的压力为零时，仅由重力充当向心力，对应的速度υ2为越过圆环最高点的最小速度，对应的高度h1为最低高度，由机械能守恒定律及圆周运动知识有：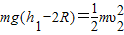
③
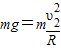④
联立③④解得：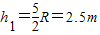
（3）由于h'＜h1，故球在还没有到达顶端前即与环脱离，设脱离圆环时的位置半径与竖直方向的夹角为α，选轨道最低点为零势点，由机械能守恒定律及圆周运动知识有：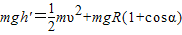
⑤
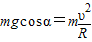⑥
联立⑤⑥解得：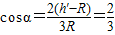
答：（1）小球滑至圆环顶点时对环的压力为40N．
（2）小球至少应从2.5m高处由静止滑下才能越过圆环最高点．
（3）小球从h'=2m处由静止滑下时，脱离圆环的位置和圆心的连线与竖直方向夹角的余弦为
．
点评：本题综合考查了牛顿第二定律和机械能守恒定律，综合性较强，关键抓住小球运动的临界状态，运用牛顿第二定律和机械能守恒定律进行求解．
（2）小球通过最高点的临界情况是弹力为零，根据重力提供向心力求出最高点的临界速度，再根据机械能守恒定律求出小球初位置的高度．
（3）由于h'＜h1，故球在还没有到达顶端前即与环脱离，脱离的瞬间，重力沿半径方向上的合力提供向心力，结合牛顿第二定律和机械能守恒定律求出脱离圆环的位置和圆心的连线与竖直方向夹角的余弦．
解答：解：（1）设小球滑至环顶时的速度为υ1，所受环的压力为N．
小球运动过程中机械能守恒：
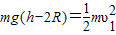①在顶点由圆周运动的知识有：
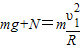②联立①②解得：
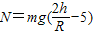（代入数值解得：
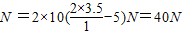
由牛顿第三定律知小球对环的压力大小为：N'=N=40N
（2）当圆环对小球的压力为零时，仅由重力充当向心力，对应的速度υ2为越过圆环最高点的最小速度，对应的高度h1为最低高度，由机械能守恒定律及圆周运动知识有：
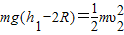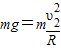③④联立③④解得：
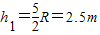
（3）由于h'＜h1，故球在还没有到达顶端前即与环脱离，设脱离圆环时的位置半径与竖直方向的夹角为α，选轨道最低点为零势点，由机械能守恒定律及圆周运动知识有：
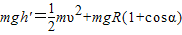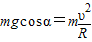⑤⑥联立⑤⑥解得：
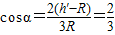
答：（1）小球滑至圆环顶点时对环的压力为40N．
（2）小球至少应从2.5m高处由静止滑下才能越过圆环最高点．
（3）小球从h'=2m处由静止滑下时，脱离圆环的位置和圆心的连线与竖直方向夹角的余弦为
．点评：本题综合考查了牛顿第二定律和机械能守恒定律，综合性较强，关键抓住小球运动的临界状态，运用牛顿第二定律和机械能守恒定律进行求解．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图所示，质量M=8kg的长木板放在光滑水平面上，在长木板的右端施加一水平恒力F=8N，当长木板向右运动速率达到v1=10m/s时，在其右端有一质量m=2kg的小物块（可视为质点）以水平向左的速率v2=2m/s滑上木板，物块与长木板间的动摩擦因数μ=0.2，小物块始终没离开长木板，g取10m/s2，求：
如图，质量M=8kg的小车停放在光滑水平面上，在小车右端施加一水平恒力F=8N．当小车向右运动速度达到3m/s时，在小车的右端轻放一质量m=2kg的小物块，物块与小车间的动摩擦因数μ=0.2，假定小车足够长，试求：
如图所示，质量M=8kg的长木板放在光滑水平面上，在长木板的右端施加一水平恒力F=8N，当长木板向右运动速率达到v1=7m/s时，在其右端有一质量m=2kg的小物块（可视为质点）以水平向左的速率v2=2m/s滑上木板，物块与长木板间的动摩擦因数μ=0.2，小物块始终没离开长木板，g取10m/s2，求：
如图所示，一质量m=2kg的小物块静止放在水平面上的A点，t=0时，物块在水平恒力F的作用下由静止开始运动．1s末到达B点时速度为8m/s，在B点立即撤去恒力F，最后在3s末停在C点，重力加速度取g=l0m/s2，求：