题目内容
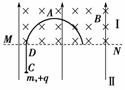
如图，一质量为m、电荷量为＋q的带电小环套在光滑轨道上，环状轨道的半径为R，直轨道长度为R.以水平线MN为界，空间分为两个区域，区域Ⅰ为磁感应强度为B的水平向里的匀强磁场，区域Ⅰ和Ⅱ有竖直向上的匀强电场．将小环在直轨道CD下端的C点无初速度释放(已知区域Ⅰ和Ⅱ的匀强电场场强大小为E＝2mg/q，重力加速度为g)，求：
(1)小环在第一次通过轨道最高点A时速度vA的大小；
(2)小环在第一次通过轨道最高点A时受到的轨道压力．
解析：(1)小环从C到A的过程中，由动能定理有
mv
＝(qE－mg)×(R＋R)，
解得vA＝2
.
(2)小环在A点时，受力分析如图所示，
由牛顿第二定律有
FN＋mg－qE－qvAB＝m
，
解得FN＝5mg＋2qB，
方向竖直向下．
答案：(1)2
(2)5mg＋2qB，竖直向下
练习册系列答案
怎样学好牛津英语系列答案
相关题目
一半径为R 的绝缘光滑1/4圆弧与绝缘光滑水平面p M相切于p点，平面p M处于水平向左电场强度为E的匀强电场中，如右图所示．一质量为m、电何量为q的可视为质点的物块从圆弧某一高度由静止滑下，刚滑到p点的速度为V．求：
如图，一质量为m，电荷量为e的质子从静止开始经加速电压U加速后，紧挨A板水平进入竖直方向的偏转电场中，已知A、B板的长度及板间距离都是L，A板电势比B板电势高2U，紧挨A、B的右侧有平面直角坐标系，坐标原点与A板右端重合，第四象限有垂直纸面向里的匀强磁场，质子在匀强磁场中运动后刚好垂直x轴射出磁场．求：
（1）试求小球释放过程中电势能的最大变化量？
、质量为m、电量为q=Q/2。试求：
