题目内容
8. 随着时代的不断发展,快递业发展迅猛,大量的快件需要分拣.为了快件的安全,某网友发明了一个缓冲装置,其理想模型如图所示.劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间有恒定的滑动摩擦力作用,轻杆向下移动一定距离后才停下,保证了快件的安全.一质量为m的快件从弹簧上端l处由静止释放,沿斜面下滑后与轻杆相撞,轻杆与槽间最大静摩擦力等于滑动摩擦力,大小为f=mg,不计快件与斜面间的摩擦.
随着时代的不断发展,快递业发展迅猛,大量的快件需要分拣.为了快件的安全,某网友发明了一个缓冲装置,其理想模型如图所示.劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间有恒定的滑动摩擦力作用,轻杆向下移动一定距离后才停下,保证了快件的安全.一质量为m的快件从弹簧上端l处由静止释放,沿斜面下滑后与轻杆相撞,轻杆与槽间最大静摩擦力等于滑动摩擦力,大小为f=mg,不计快件与斜面间的摩擦.(1)求快件与弹簧相撞时的速度大小.
(2)若弹簧的劲度系数为k=$\frac{4mg}{l}$,求轻杆开始移动时,弹簧的压缩量x1.
(3)已知弹簧的弹性势能表达式为Ep=$\frac{1}{2}k{x^2}$,其中k为劲度系数,x为弹簧的形变量.试求(2)情况下,轻杆向下运动时快件的加速度a,以及轻杆向下移动的最大距离x2.
分析 (1)快件向下运动的过程中机械能守恒,由此即可求出快件与弹簧相撞时的速度大小;
(2)轻杆开始移动时,根据胡克定律求出弹簧的压缩量;
(3)根据牛顿第二定律求出快件的加速度;则快件开始运动到杆刚刚开始运动的过程中,重力和弹簧的弹力做功,对快件由动能定理快件的速度;快件从撞击到停止的过程中由运动学列出等式求解.
解答 解:(1)由于不计快件与斜面间的摩擦,所以快件向下运动的过程中机械能守恒,得:
$mglsinθ=\frac{1}{2}m{v}_{1}^{2}$ ①
所以:v1=$\sqrt{2glsin30°}$=$\sqrt{gl}$
(2)轻杆开始移动时,弹簧的弹力F=kx1 ②
且F=f=mg ③
解得 x1=$\frac{f}{k}$=$\frac{mg}{\frac{4mg}{l}}=\frac{l}{4}$
(3)轻杆开始移动时,弹簧的弹力F=kx=$\frac{4mg}{l}×\frac{l}{4}=mg$ ④
沿斜面的方向,选取向下为正方向,由牛顿第二定律得:ma=mgsinθ-F ⑤
联立④⑤得:a=$-\frac{1}{2}g$
负号表示方向向上.
设杆移动前快件对弹簧所做的功为W,则快件开始运动到杆刚刚开始运动的过程中,对快件由动能定理得:
$mg(l+{x}_{1})•sinθ-W=\frac{1}{2}m{v}^{2}-0$ ⑥
由于快件对弹簧所做的功为W转化为弹簧的弹性势能,即:W=Ep=$\frac{1}{2}k{x}_{1}^{2}$ ⑦
联立得:$v=\sqrt{gl}$
快件向下做减速运动,有运动学的公式得:$2a{x}_{2}=0-{v}^{2}$
所以:${x}_{2}=\frac{{v}^{2}}{-2a}=l$
答:(1)求快件与弹簧相撞时的速度大小是$\sqrt{gl}$.
(2)若弹簧的劲度系数为k=$\frac{4mg}{l}$,轻杆开始移动时,弹簧的压缩量是$\frac{l}{4}$.
(3)已知弹簧的弹性势能表达式为Ep=$\frac{1}{2}k{x^2}$,其中k为劲度系数,x为弹簧的形变量.在(2)情况下,轻杆向下运动时快件的加速度大小是$\frac{1}{2}g$,方向向上,轻杆向下移动的最大距离x2是l.
点评 正缓冲装置是一种实用装置,在生产和生活中有着广泛的应用,本题就是根据某种缓冲装置改编的一道物理试题,试题设计新颖,物理思想深刻.正确解答这道试题,要求考生具有扎实的高中物理基础以及很强的分析和解决问题的能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 在如图所示的电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,下列说法正确的是( )
在如图所示的电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,下列说法正确的是( )| A. | I减小,U1变大 | B. | U2变大,U3减小 | C. | I减小,U2变大 | D. | U1减小,U3减小 |
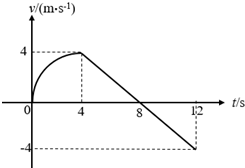 某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )
某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )| A. | 质点在第一个4 s内的平均速度和在第二个4 s内的平均速度大小相等 | |
| B. | t=12 s时,质点的位移最大 | |
| C. | 质点在t=6 s时的加速度与t=10 s时的加速度大小相等,方向相反 | |
| D. | 质点在这12 s内的平均速度约为3 m/s |
 如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.则地球绕太阳转动的角速度与行星绕太阳转动的角速度之比值为( )
如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.则地球绕太阳转动的角速度与行星绕太阳转动的角速度之比值为( )| A. | $\sqrt{{{tan}^3}θ}$ | B. | $\sqrt{{{sin}^3}θ}$ | C. | $\sqrt{\frac{1}{{{{sin}^3}θ}}}$ | D. | $\sqrt{\frac{1}{{{{tan}^3}θ}}}$ |

| A. | 弹簧的弹力等于木箱受到的摩擦力与人所受的摩擦力之和 | |
| B. | 图甲中木箱受到的摩擦力小于图乙中木箱受到的摩擦力 | |
| C. | 图甲中男孩受到的合力小于图乙中男孩受到的合力 | |
| D. | 图甲中男孩受到的合力大于图乙中男孩受到的合力 |
 某一款读卡器的原理可简化成如图所示的模型,水平操作台上叠放有一堆卡片,每一张卡片的质量均为m.滚轮以竖直向下的力压在第1张卡片上,并沿逆时针方向转动,确保第1张卡片与第2张卡片之间有相对滑动.设最大静摩擦力与滑动摩擦力相同,滚轮与第l张卡片之间的动摩擦因数为μ1,卡片之间、卡片与桌面之间的动摩擦因数均为μ2,且有μ1>μ2,则下列说法正确的是( )
某一款读卡器的原理可简化成如图所示的模型,水平操作台上叠放有一堆卡片,每一张卡片的质量均为m.滚轮以竖直向下的力压在第1张卡片上,并沿逆时针方向转动,确保第1张卡片与第2张卡片之间有相对滑动.设最大静摩擦力与滑动摩擦力相同,滚轮与第l张卡片之间的动摩擦因数为μ1,卡片之间、卡片与桌面之间的动摩擦因数均为μ2,且有μ1>μ2,则下列说法正确的是( )| A. | 第1张卡片受到滚轮的摩擦力向左 | |
| B. | 最后一张卡片受到水平桌面的摩擦力向左 | |
| C. | 下一张卡片受到上一张卡片的摩擦力一定向左 | |
| D. | 任意两张卡片之间均可能发生相对滑动 |
 如图所示,某人造地球卫星绕地球沿椭圆轨道运动,从A到B和从C到D的运动过程中,卫星与地球的连线扫过的面积相等,下列说法正确的是( )
如图所示,某人造地球卫星绕地球沿椭圆轨道运动,从A到B和从C到D的运动过程中,卫星与地球的连线扫过的面积相等,下列说法正确的是( )| A. | 从A到B的运动时间等于从C到D的运动时间 | |
| B. | 从A运动到B的过程中卫星的动能保持不变 | |
| C. | 从C运动到D的过程中引力势能不断减小 | |
| D. | 从B运动到C的过程中地球对卫星的引力一直不做功 |
 小船在静水中速度为4m/s,它在宽为200m,流速为3m/s的河中渡河,如图所示
小船在静水中速度为4m/s,它在宽为200m,流速为3m/s的河中渡河,如图所示