题目内容
天文学家发现了一颗太阳系外行星,其半径约为地球的2倍,质量约为地球的6倍;并环绕着一颗红矮星运行,公转周期约为地球公转周期的1/200,公转半径约为日地距离的1/50.设该行星表面的重力加速度为g1,地球表面重力加速度为g2,该红矮星的质量为M1,太阳质量为M2.假定该行星和地球公转轨迹为圆,且不考虑自转.以下估算正确的是( )A..g1和g2的比值约为3:2
B..g1和g2 的比值约为3:1
C.M1和M2的比值约为3:1
D.M1和M2的比值约为8:25
【答案】分析:(1)星球表面的物体受到的重力等于星球对它的万有引力,求出重力加速度的表达式,然后求出两加速度之比.
(2)行星绕恒星做圆周运动所需向心力由万有引力提供,由牛顿第二定律列方程求出恒星质量的表达式,然后求出红矮星与太阳的质量之比.
解答:解:(1)设某物体质量为m,设行星质量为M,行星半径为r,
物体受到的重力等于万有引力,即:G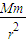 =mg,则重力加速度g=
=mg,则重力加速度g=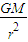 ,
,
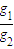 =
= =
= =
=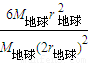 =
= ,故A正确,B错误;
,故A正确,B错误;
(2)行星绕红矮星做圆周运动,由牛顿第二定律得:
G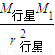 =M行星
=M行星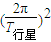 r行星,红矮星质量:M1=
r行星,红矮星质量:M1= ;
;
地球绕太阳做圆周运动,由牛顿第二定律得:
G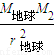 =M地球
=M地球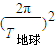 r地球,太阳质量:M2=
r地球,太阳质量:M2= ,
,
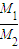 =
= =
= =
= =
=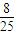 ,
,
故C错误,D正确;
故选AD.
点评:本题难度不是很大,熟练应用万有引力公式、牛顿定律即可正确解题.
(2)行星绕恒星做圆周运动所需向心力由万有引力提供,由牛顿第二定律列方程求出恒星质量的表达式,然后求出红矮星与太阳的质量之比.
解答:解:(1)设某物体质量为m,设行星质量为M,行星半径为r,
物体受到的重力等于万有引力,即:G
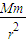 =mg,则重力加速度g=
=mg,则重力加速度g=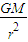 ,
,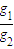 =
= =
= =
=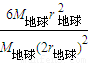 =
= ,故A正确,B错误;
,故A正确,B错误;(2)行星绕红矮星做圆周运动,由牛顿第二定律得:
G
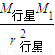 =M行星
=M行星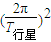 r行星,红矮星质量:M1=
r行星,红矮星质量:M1= ;
;地球绕太阳做圆周运动,由牛顿第二定律得:
G
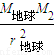 =M地球
=M地球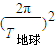 r地球,太阳质量:M2=
r地球,太阳质量:M2= ,
,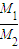 =
= =
= =
= =
=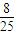 ,
,故C错误,D正确;
故选AD.
点评:本题难度不是很大,熟练应用万有引力公式、牛顿定律即可正确解题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目