题目内容
如图所示,一根均质绳质量为M,其两端固定在天花板上的A、B两点,在绳的中点悬挂一重物,质量为m,悬挂重物的绳PQ质量不计.设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角,则 等于( )
等于( )
A.

B.

C.

D.

【答案】分析:以整体为研究对象,根据平衡条件分析端点处对绳子的拉力与总重力的关系式;对左半边绳子研究,得到端点和中点绳子的拉力的关系式;再采用比例求解.
解答:解:设绳子端点处和中点处绳子张力分别为F1、F2.
对整体研究,根据平衡条件得
F1cosα= ①
①
对左半边绳子研究得
F1cosα=F2cosβ+ ②
②
F1sinα=F2sinβ ③
由①②得到 F2cosβ= ④
④
则由③:①得 tanα= ⑤
⑤
由③:④得 tanβ= ⑥
⑥
所以由③⑤⑥联立得 =
=
故选A
点评:本题是力平衡问题,难点存在如何选择研究对象和如何运用数学知识变形求解.
解答:解:设绳子端点处和中点处绳子张力分别为F1、F2.

对整体研究,根据平衡条件得
F1cosα=
 ①
①对左半边绳子研究得
F1cosα=F2cosβ+
 ②
②F1sinα=F2sinβ ③
由①②得到 F2cosβ=
 ④
④则由③:①得 tanα=
 ⑤
⑤由③:④得 tanβ=
 ⑥
⑥所以由③⑤⑥联立得
 =
=
故选A
点评:本题是力平衡问题,难点存在如何选择研究对象和如何运用数学知识变形求解.

练习册系列答案
相关题目
 如图所示,一根均质绳质量为M,其两端固定在天花板上的A、B两点,在绳的中点悬挂一重物,质量为m,悬挂重物的绳PQ质量不计.设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角,则
如图所示,一根均质绳质量为M,其两端固定在天花板上的A、B两点,在绳的中点悬挂一重物,质量为m,悬挂重物的绳PQ质量不计.设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角,则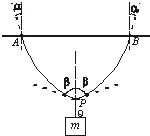 如图所示,一根均质绳质量为M,其两端固定在天花板上的A、B两点,在绳的中点悬挂一重物,质量为m,悬挂重物的绳PQ质量不计.设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角,则
如图所示,一根均质绳质量为M,其两端固定在天花板上的A、B两点,在绳的中点悬挂一重物,质量为m,悬挂重物的绳PQ质量不计.设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角,则 等于
等于
 B.
B.
 D.
D.

 = .
= .