题目内容
如图所示，MN为半圆形玻璃砖的对称轴，O为玻璃砖圆心，某同学在与MN平行的直线上插上两根大头针P1、P2，在MN上插大头钱P3，从P3一侧透过玻璃砖观察P1、P2的像，调整P3位置使P3能同时挡住P1、P2的像，确定了的P3位置如图所示，他测得玻璃砖直径D=8cm，P1P2连线与MN之间的距离d1=2cm，P3到O的距离d2=6.92cm．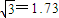
，求该玻璃砖的折射率．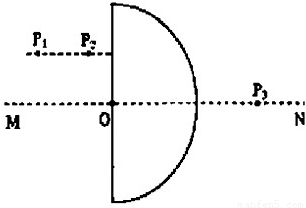
【答案】分析：作出光路图，由数学知识求出光线射到圆弧面上的入射角i和折射角r，由折射定律n=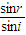
求出折射率．
解答：解：作出光路图如图．
则 sini=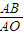
=
=
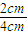，得i=30°，∠OAB=60°
=
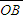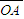sin60°=4cm×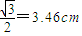
根据几何关系得
=
-
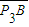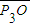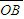=d2-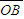
=6.92cm-3.46cm=3.46cm
tan∠BAP3=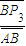
=
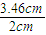=1.73，得∠BAP3=60°
故r=180°-∠OAB-∠BAP3=60°
由折射定律得n=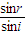
=
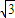=1.73
答：该玻璃砖的折射率是1.73．
点评：本题的难点是求入射角和折射角，在作出光路图的基础上，运用几何知识求解．
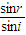求出折射率．解答：解：作出光路图如图．
则 sini=
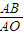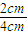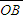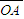==，得i=30°，∠OAB=60°=sin60°=4cm×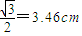根据几何关系得
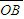=-=d2-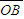=6.92cm-3.46cm=3.46cmtan∠BAP3=
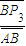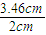==1.73，得∠BAP3=60°故r=180°-∠OAB-∠BAP3=60°
由折射定律得n=
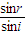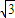==1.73答：该玻璃砖的折射率是1.73．
点评：本题的难点是求入射角和折射角，在作出光路图的基础上，运用几何知识求解．
练习册系列答案
阅读快车系列答案
相关题目
半径为a的圆形区域内有均匀磁场，磁感强度为B=0.3T，磁场方向垂直纸面向里，半径为b的金属圆环与磁场同心放置，磁场与环面垂直，其中a=0.2m，b=0.4m，金属环上分别接有灯L1、L2，两灯的电阻均为R=1Ω，一金属棒MN与金属环接触良好，棒单位长度的电阻R0=0.5Ω/m，金属环的电阻忽略不计．求：
如图所示，MN是位于水平平面内的光屏，放在水平面上的半圆柱形玻璃砖的平面部分ab 与屏平行，由光源S发出的一束白光从半圆沿半径射入玻璃砖，通过圆心O再射到屏上，在竖直平面内以O点为圆心沿逆时针方向缓缓转动玻璃砖，在光屏上出现了彩色光带，当玻璃砖转动角度大于某一值，屏上彩色光带中的某种颜色的色光首先消失，有关彩色光的排列顺序和最先消失的色光是（ ）
（2013?天津模拟）如图所示，MN和PQ为固定在绝缘水平面上两平行光滑金属导轨，导轨左端MP间接有阻值为R1=2Ω导线；导轨右端接有与水平轨道相切、半径r=0.5m内壁光滑的半圆金属轨道．导轨间距L=0.4m，电阻不计．导轨所在平面abcd区域内有竖直向上B=0.5T的匀强磁场．导轨上长度也为0.4m、质量m=0.6kg、电阻R2=1Ω的金属棒AB以v0=6m/s速度进入磁场区域，离开磁场区域后恰好能到达半圆轨道的最高点，运动中金属棒始终与导轨保持良好接触．已知重力加速度g=10m/s2．求：
如图所示，倾角为θ宽度为d长为L的光滑倾斜导轨C1D1、C2D2顶端接有可变电阻R0，L足够长，倾斜导轨置于垂直导轨平面斜向左上方的匀强磁场中，磁感应强度为B，C1A1B1、C2A2B2为绝缘轨道，由半径为R处于竖直平面内的光滑半圆环A1B1、A2B2和粗糙的水平轨道C1A1、C2A2组成，粗糙的水平轨道长为S，整个轨道对称．在导轨顶端垂直于导轨放一根质量为m、电阻不计的金属棒MN，使其从静止开始自由下滑，不考虑金属棒MN经过接点A1A2、C1C2处时机械能的损失，整个运动过程中金属棒始终保持水平，水平导轨与金属棒MN之间的动摩擦因数为?．则：