题目内容
20. 在长方形ABCD区域内存在着垂直纸面向里的匀强磁场,AB=2AD,A处有一个放射源,向四周均匀发射速度大小相等、方向平行于纸的同种带电粒子.DC边上只有在E、F之间才有粒子穿出,不考虑粒子之间的相互作用.已知FA和BA夹角为30°.试回答下列问题:
在长方形ABCD区域内存在着垂直纸面向里的匀强磁场,AB=2AD,A处有一个放射源,向四周均匀发射速度大小相等、方向平行于纸的同种带电粒子.DC边上只有在E、F之间才有粒子穿出,不考虑粒子之间的相互作用.已知FA和BA夹角为30°.试回答下列问题:(1)粒子带正电还是带负电.
(2)从E飞出的粒子与从F飞出的粒子在磁场中运动时间之比.
(3)若其他条件不变,仅将磁场的磁感应强度变为原来的k倍,要使CB之间都有粒子射出,那么k的最大值是多少?
分析 作出粒子运动轨迹图,沿AD方向的粒子通过E点,这是割线,而F点必为切线;
根据几何关系,可求解;
只要粒子能够从C点通过,粒子在CB边上都能射出由几何关系及洛伦兹力提供向心力联立,可求解
解答 解:(1)粒子轨迹如图所示,根据左手定则力与运动关系可知,粒子带正电
(2)根据几何关系可知,∠AO2F=60°,设粒子做匀速圆周运动的轨迹半径为R,AD=l,则R=2l,
所以∠AO1E=30°,又因为粒子在磁场中运动时间t=$\frac{θ}{2π}T$,(θ是轨道所在圆心,T为周期),则从E、F飞出粒子在磁场中运动时间之比:tE:tF=∠AO1E:∠AO2F=1:2
(3)只要粒子能够从C点通过,粒子在CB边上都能射出,设粒子从C点射出时轨道半径为r,由几何关系可知,r=2.5l
又:$qBv=\frac{m{v}^{2}}{r}$,故$r=\frac{mv}{qB}$
故:2l:2.5l=kB:B,则k=0.8
答:(1)粒子带正电;(2)从E飞出的粒子与从F飞出的粒子在磁场中运动时间之比为1:2.
(3)k的最大值是0.8.
点评 本题考查了粒子在磁场中的运动,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,分析清楚粒子运动过程、作出粒子运动轨迹是正确解题的前提与关键,几何知识即可正确解题.

练习册系列答案
相关题目
8. 如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )
如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )
 如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )
如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )| A. | A和B、C和D处于相对静止状态 | |
| B. | B点相对A点运动趋势的方向与B点运动方向相反 | |
| C. | D点受到摩擦力的方向与D点的运动方向相同 | |
| D. | A点受到摩擦力的方向与A点的运动方向相同 |
12. 如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )
如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )
 如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )
如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )| A. | A灯变亮,B灯变暗 | B. | A灯变暗,B灯变亮 | ||
| C. | A灯得功率可能为原来的$\frac{1}{2}$ | D. | A灯得功率可能为原来的$\frac{3}{4}$ |
9.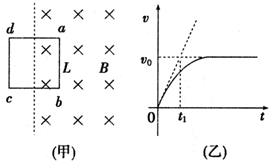 一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )
一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )
 一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )
一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )| A. | $\frac{mR{v}_{0}}{{t}_{1}N{B}_{0}{L}^{3}}$ | B. | $\frac{2mR{v}_{0}}{{t}_{1}N{B}_{0}{L}^{2}}$ | ||
| C. | $\frac{mR{v}_{0}}{{t}_{1}{N}^{2}{B}_{0}{L}^{2}}$ | D. | $\frac{2mR{v}_{0}}{{t}_{1}{N}^{2}{B}_{0}{L}^{3}}$ |
10. 质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )
 质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )| A. | $\frac{2mg}{M+4m}$ | B. | $\frac{2mg}{M+2m}$ | C. | $\frac{mg}{2M}$ | D. | $\frac{mg}{M+m}$ |
 利用图中所示的装置可以研究自由落体运动,实验中需要调整好仪器,接通打点计时器的电源,松开纸带,使重物下落.打点计时器会在纸带上打出一系列的小点.
利用图中所示的装置可以研究自由落体运动,实验中需要调整好仪器,接通打点计时器的电源,松开纸带,使重物下落.打点计时器会在纸带上打出一系列的小点. 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,设物体受到的最大静摩擦力等于滑动摩擦力,取g=10m/s2.(sin37°=0.6,cos37°=0.8)试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,设物体受到的最大静摩擦力等于滑动摩擦力,取g=10m/s2.(sin37°=0.6,cos37°=0.8)试求: 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子,在放射源右边有一垂直于x轴放置的很薄的挡板,挡板与xOy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速率为v,MN的长度为L.(粒子不计重力).若在整个空间加一方向垂直纸面向里匀强磁场,
如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子,在放射源右边有一垂直于x轴放置的很薄的挡板,挡板与xOy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速率为v,MN的长度为L.(粒子不计重力).若在整个空间加一方向垂直纸面向里匀强磁场, 从阴极K发射的电子经电势差U0=4500V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm,间距d=4cm的平行金属板AB之后,在离金属板边缘L2=75cm处放置一个直径D=20cm的带有记录纸的圆筒(如图所示),整个装置放在真空内,电子发射的初速度不计.已知电子质量m=0.9×10-30kg.
从阴极K发射的电子经电势差U0=4500V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm,间距d=4cm的平行金属板AB之后,在离金属板边缘L2=75cm处放置一个直径D=20cm的带有记录纸的圆筒(如图所示),整个装置放在真空内,电子发射的初速度不计.已知电子质量m=0.9×10-30kg.