题目内容
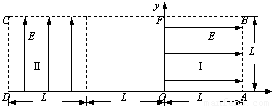
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计粒子所受重力).(1)在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置;
(2)在电场I区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置;
(3)若将左侧电场II整体水平向右移动L/4,仍使电子从ABCD区域左下角D处离开(D不随电场移动),在电场I区域内由静止释放电子的所有位置.
【答案】分析:(1)、此问分为两个过程,一是在电场Ⅰ区域的加速运动,运用能量的关系可求出加速后的速度;二是在电场Ⅱ区域内的偏转,运用类平抛的知识可求出偏转距离,从而得到电子离开ABCD区域的位置.
(2)、首先设出释放点的坐标,在运用在电场I中的加速和在电场II中的类平抛运动,计算出表示xy的乘积的方程,满足此式的点即为符合要求的点.
(3)、该问分为三个阶段,一是在电场I中的直线加速运动,二是在电场II中的类平抛运动,三是从电场II射出后的匀速直线运动,结合第二问的解题思路,可求出结果.
解答:解:(1)设电子的质量为m,电量为e,在电场I中释放后将做出速度为零的匀加速直线运动,出区域I时的速度为vo,接着进入电场II做类平抛运动,假设电子从CD边射出,出射点纵坐标为y,对电子的整个运动过程运用动能定理和匀变速直线运动公式有:eEL= mv2,
mv2,
在电场Ⅱ区域内的偏转,L=vt,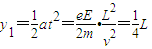 ,方向向下,
,方向向下,
故: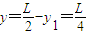
所以位置坐标(-2L, L)
L)
(2)设释放位置坐标为(x,y),在电场I中电子被加速到v1,然后进入电场II做类平抛运动,并从D点离开,有:eEx= mv2,
mv2,
L=vt,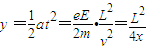 ,所以满足
,所以满足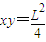 方程的点即为释放点的位置
方程的点即为释放点的位置
(3)设释放位置坐标为(x,y),eEx= mv2,在电场I中加速到v2,进入电场II后做类平抛运动,在高度为y′处离开电场II时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有:
mv2,在电场I中加速到v2,进入电场II后做类平抛运动,在高度为y′处离开电场II时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有:
L=vt1,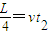 ,
,
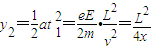 ,
,
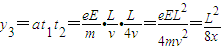 ,
,
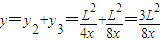 ,
,
所以满足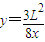 方程的点即为释放点的位置.
方程的点即为释放点的位置.
答:(1)在该区域AB边的中点处由静止释放电子,电子从(-2L,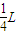 )离开ABCD区域.
)离开ABCD区域.
(2)在电场I区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,所有释放点为满足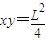 的位置.
的位置.
(3)若将左侧电场II整体水平向右移动在电场I区域内由静止释放电子的所有位置,在电场I区域内由静止释放电子的所有位置为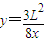 .
.
点评:本题考核了带电粒子在简化的电子枪模型中的运动情况,是一道拓展型试题,与常见题所不同的是,一般试题是已知电子的出发点,然后求电子在电场作用下运动过程中的轨迹或离开电场的出射点位置,而本题则是反其道而行之,是规定了电子的出射点,要反推出在何处发出电子才能满足所述要求.从内容看,该题涉及的是电子在电场中的运动,这部分知识学生相对比较熟悉,也是经常训练的题型之一,只不过本题作了拓展.
(2)、首先设出释放点的坐标,在运用在电场I中的加速和在电场II中的类平抛运动,计算出表示xy的乘积的方程,满足此式的点即为符合要求的点.
(3)、该问分为三个阶段,一是在电场I中的直线加速运动,二是在电场II中的类平抛运动,三是从电场II射出后的匀速直线运动,结合第二问的解题思路,可求出结果.
解答:解:(1)设电子的质量为m,电量为e,在电场I中释放后将做出速度为零的匀加速直线运动,出区域I时的速度为vo,接着进入电场II做类平抛运动,假设电子从CD边射出,出射点纵坐标为y,对电子的整个运动过程运用动能定理和匀变速直线运动公式有:eEL=
 mv2,
mv2,在电场Ⅱ区域内的偏转,L=vt,
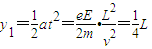 ,方向向下,
,方向向下,故:
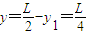
所以位置坐标(-2L,
 L)
L)(2)设释放位置坐标为(x,y),在电场I中电子被加速到v1,然后进入电场II做类平抛运动,并从D点离开,有:eEx=
 mv2,
mv2,L=vt,
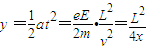 ,所以满足
,所以满足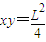 方程的点即为释放点的位置
方程的点即为释放点的位置(3)设释放位置坐标为(x,y),eEx=
 mv2,在电场I中加速到v2,进入电场II后做类平抛运动,在高度为y′处离开电场II时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有:
mv2,在电场I中加速到v2,进入电场II后做类平抛运动,在高度为y′处离开电场II时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有:L=vt1,
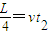 ,
,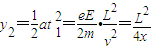 ,
,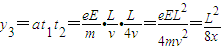 ,
,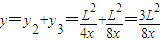 ,
,所以满足
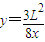 方程的点即为释放点的位置.
方程的点即为释放点的位置.答:(1)在该区域AB边的中点处由静止释放电子,电子从(-2L,
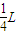 )离开ABCD区域.
)离开ABCD区域.(2)在电场I区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,所有释放点为满足
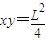 的位置.
的位置.(3)若将左侧电场II整体水平向右移动在电场I区域内由静止释放电子的所有位置,在电场I区域内由静止释放电子的所有位置为
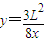 .
.点评:本题考核了带电粒子在简化的电子枪模型中的运动情况,是一道拓展型试题,与常见题所不同的是,一般试题是已知电子的出发点,然后求电子在电场作用下运动过程中的轨迹或离开电场的出射点位置,而本题则是反其道而行之,是规定了电子的出射点,要反推出在何处发出电子才能满足所述要求.从内容看,该题涉及的是电子在电场中的运动,这部分知识学生相对比较熟悉,也是经常训练的题型之一,只不过本题作了拓展.

练习册系列答案
相关题目
 (2008?上海)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力).
(2008?上海)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力). 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计粒子所受重力).在该区域AB边的中点处由静止释放电子,求:
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计粒子所受重力).在该区域AB边的中点处由静止释放电子,求:
 力),现在该区域AB边的中点处由静止释放一电子,已知电子质量为m,带电量为e,试求:
力),现在该区域AB边的中点处由静止释放一电子,已知电子质量为m,带电量为e,试求: 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的第一象限,存在以x轴y轴及双曲线y=
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的第一象限,存在以x轴y轴及双曲线y=