Question

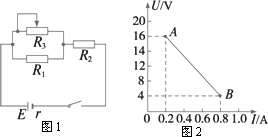
在图1所示电路中，R₁、R₂均为定值电阻，且R₁＝100 Ω，R₂的阻值未知，R₃是一滑动变阻器，在其滑键从最左端滑至最右端的过程中，测得电源的端电压随电流I的变化图线图2所示，其中图线上的A、B两点是滑键在变阻器的两个不同端点时分别得到的，求：

(1)电源的电动势和内电阻；

(2)定值电阻R₂的阻值；

(3)滑动变阻器R₃的最大值；

(4)上述过程中R₁上得到的最大功率以及电源的最大输出功率．

Answer 1

答案：
解析：

　　解：(1)由闭合电路欧姆定律得E＝U＋Ir

　　将图象中A、B两点的电压和电流代入得E＝16＋0.2r；E＝4＋0.8r

　　联立解得E＝20 V；r＝20 Ω．

　　(2)当R₃的滑键自左向右滑时，R₃阻值变小，使电路总电阻变小，而总电流变大，由此可知，图线上的A、B两点是滑键分别位于最左端和最右端时所得到的，当滑键位于最右端时，R₃＝0，R₁被短路，外电路总电阻即为R₂，故由B点的U、I值可求出R₂．

　　R₂＝＝Ω＝5 Ω．

　　(3)当滑键在最左端时，其阻值最大，并对应着图线上的A点，故由A点的U、I值可求出此时外电路总电阻，再根据串、并联电路的规律可求出R₃的最大值．

　　R_总＝Ω＝80 Ω；又R_总＝＋R₂

　　代入数值解得滑动变阻器的最大值R₃＝300 Ω．

　　(4)当R₁消耗的功率最大时，它两端电压应最大，由U_R1＝E－I(R₂＋r)知，这时电路的总电流I应最小，故应把滑动变阻器的阻值调到最大，再结合上面求出有关数据，便不难求出R₁消耗的最大功率．

　　当R₃＝300 Ω时，I＝A＝0.2 A

　　此时R₁两端的电压为：U₁＝I·＝0.2×75 V＝15 V

　　则R₁消耗的最大功率为：P₁m＝W＝2.25 W

　　又当R_外＝r时，电源输出功率最大，即有P_m＝＝W＝5 W．