题目内容
钢质小球A的质量为m1=0.35kg,橡皮泥小球B的质量为m2=0.15kg,在某高度处将A和B先后从静止释放.小球A与水平地面弹性碰撞后向上弹回,在释放点的下方且与释放点距离为H=5m的地方恰好与正在下落的小球B发生正碰粘在一起,碰撞时间极短.重力加速度g=10m/s2,试求:(1)小球碰撞后上升的最大高度.
(2)碰撞后AB两球增加的内能的最大值.
【答案】分析:(1)由于AB是从同一高度释放的,并且碰撞过程中没有能量的损失,根据机械能守恒可以求得碰撞时的速度的大小,再根据A、B碰撞过程中动量守恒,可以求得碰后的速度大小,进而求可以得A、B碰撞后B上升的最大高度;
(2)损失的机械能全部转化成内能就为二球增加的内能最大值.
解答:解:小球在释放处的下方与释放出距离为h=5m的地方的速度大小均为v,
根据机械能守恒定律得:
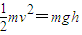
解得:v=10m/s
A球向上,B球向下.碰撞后粘在一起的共同速度为V,由动量守恒:m1v1-m2v2=(m1+m2)V,解出V=4m/s.
碰撞后上升的最大高度: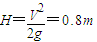
损失的机械能全部转化成内能就为二球增加的内能最大值: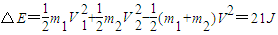
答:(1)小球碰撞后上升的最大高度为0.8m.
(2)碰撞后AB两球增加的内能的最大值为21J.
点评:本题考查的是机械能守恒的应用,同时在碰撞的过程中物体的动量守恒,在利用机械能守恒和动量守恒的时候一定注意各自的使用条件,将二者结合起来应用即可求得本题.
(2)损失的机械能全部转化成内能就为二球增加的内能最大值.
解答:解:小球在释放处的下方与释放出距离为h=5m的地方的速度大小均为v,
根据机械能守恒定律得:
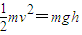
解得:v=10m/s
A球向上,B球向下.碰撞后粘在一起的共同速度为V,由动量守恒:m1v1-m2v2=(m1+m2)V,解出V=4m/s.
碰撞后上升的最大高度:
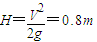
损失的机械能全部转化成内能就为二球增加的内能最大值:
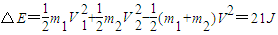
答:(1)小球碰撞后上升的最大高度为0.8m.
(2)碰撞后AB两球增加的内能的最大值为21J.
点评:本题考查的是机械能守恒的应用,同时在碰撞的过程中物体的动量守恒,在利用机械能守恒和动量守恒的时候一定注意各自的使用条件,将二者结合起来应用即可求得本题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 碰撞的恢复系数的定义为c=
碰撞的恢复系数的定义为c= (2007?浙江)(1)用示波器观察频率为900Hz的正弦电压信号.把该信号接入示波器Y输入.
(2007?浙江)(1)用示波器观察频率为900Hz的正弦电压信号.把该信号接入示波器Y输入.
 =
= ,其中
,其中 和
和 分别是碰撞前两物体的速度,
分别是碰撞前两物体的速度, 和
和 分别是碰撞后两物体的速度。弹性碰撞的恢复系数
分别是碰撞后两物体的速度。弹性碰撞的恢复系数