题目内容
19. 如图所示,一个质量为2Kg的滑块在一大小为F=40N的水平恒力的作用下恰好能沿斜面向上做匀速直线运动,斜面始终静止在水平地面上,倾角θ=37o,(sin37°=0.6 cos37°=0.8 g=10m/s2).求:滑块与斜面间的滑动 摩擦因数μ的大小.
如图所示,一个质量为2Kg的滑块在一大小为F=40N的水平恒力的作用下恰好能沿斜面向上做匀速直线运动,斜面始终静止在水平地面上,倾角θ=37o,(sin37°=0.6 cos37°=0.8 g=10m/s2).求:滑块与斜面间的滑动 摩擦因数μ的大小.
分析 以滑块为研究对象受力分析,摩擦力沿斜面向下,正交分解,根据平衡条件列方程求解.
解答 解:对滑块受力分析,受到重力、水平推力、斜面的支持力和沿斜面向下的滑动摩擦力四个力的作用而做匀速直线运动,将力沿平行于斜面和垂直于斜面正交分解,在平行于斜面的方向上,有:Fcosθ-mgsinθ-μN=0,
在垂直于斜面的方向上,有:N-Fsinθ-mgcosθ=0,
代入数据解得:μ=$\frac{Fcosθ-mgsinθ}{Fsinθ+mgcosθ}=\frac{40×0.8-20×0.6}{40×0.6+20×0.8}$=0.5;
答:滑块与斜面间的滑动摩擦因数μ的大小为0.5.
点评 本题关键是受力分析后根据平衡条件并采用正交分解法列式求解.
利用正交分解方法解体的一般步骤:
①明确研究对象;
②进行受力分析;
③建立直角坐标系,建立坐标系的原则是让尽可能多的力落在坐标轴上,将不在坐标轴上的力正交分解;
④x方向,y方向分别列平衡方程求解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
9. 如图所示,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触,现将摆球a向左边拉开一小角度后释放,若两球的碰撞是弹性的,下列判断中正确的是( )
如图所示,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触,现将摆球a向左边拉开一小角度后释放,若两球的碰撞是弹性的,下列判断中正确的是( )
 如图所示,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触,现将摆球a向左边拉开一小角度后释放,若两球的碰撞是弹性的,下列判断中正确的是( )
如图所示,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触,现将摆球a向左边拉开一小角度后释放,若两球的碰撞是弹性的,下列判断中正确的是( )| A. | 第一次碰撞后的瞬间,两球的速度大小不相等 | |
| B. | 第一次碰撞后的瞬间,两球的动量大小相等 | |
| C. | 第一次碰撞后,两球的最大摆角相同 | |
| D. | 发生第二次碰撞后,两球的最大摆角与第一次碰撞后的最大摆角不相同 |
10.一列横波沿直线传播,在传播方向上选取相距1.2m的A、B两点.当波刚好到达其中某一点时,开始计时.4s内,A点完成了9次全振动,B点完成了10次全振动,则正确结论是( )
| A. | 波由A点传向B点,波速是3m/s | B. | 波由B点传向A点,波速是3m/s | ||
| C. | 波由A点传向B点,波速是0.3m/s | D. | 波由B点传向A点,波速是0.3m/s |
7.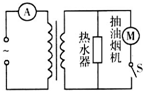 如图,理想变压器原线圈接交流电源,副线圈接热水器和抽油烟机,原副线圈的匝数比为5:1,副线圈上电源的瞬时值u=220$\sqrt{2}$sin100πt(V),开关S断开时,电流表示数是1A,开关S闭合时,电流表示数是1.2A,下列说法正确的是( )
如图,理想变压器原线圈接交流电源,副线圈接热水器和抽油烟机,原副线圈的匝数比为5:1,副线圈上电源的瞬时值u=220$\sqrt{2}$sin100πt(V),开关S断开时,电流表示数是1A,开关S闭合时,电流表示数是1.2A,下列说法正确的是( )
 如图,理想变压器原线圈接交流电源,副线圈接热水器和抽油烟机,原副线圈的匝数比为5:1,副线圈上电源的瞬时值u=220$\sqrt{2}$sin100πt(V),开关S断开时,电流表示数是1A,开关S闭合时,电流表示数是1.2A,下列说法正确的是( )
如图,理想变压器原线圈接交流电源,副线圈接热水器和抽油烟机,原副线圈的匝数比为5:1,副线圈上电源的瞬时值u=220$\sqrt{2}$sin100πt(V),开关S断开时,电流表示数是1A,开关S闭合时,电流表示数是1.2A,下列说法正确的是( )| A. | S闭合时,抽油烟机消耗的功率是220W | |
| B. | 交流电源输出电压的最大值是1100V | |
| C. | S闭合时,热水器消耗的功率减小 | |
| D. | S闭合时,热水器消耗的功率是220W |
14. 如图所示,斜面体B静置于水平桌面上,斜面上各处粗糙程度相同.一质量为M的木块A从斜面底端开始以初速度v0上滑,然后又返回出发点,此时速度为v,且v<v0,在上述过程中斜面体一直静止不动,重力加速度大小为g. 关于上述运动过程的说法,错误的是( )
如图所示,斜面体B静置于水平桌面上,斜面上各处粗糙程度相同.一质量为M的木块A从斜面底端开始以初速度v0上滑,然后又返回出发点,此时速度为v,且v<v0,在上述过程中斜面体一直静止不动,重力加速度大小为g. 关于上述运动过程的说法,错误的是( )
 如图所示,斜面体B静置于水平桌面上,斜面上各处粗糙程度相同.一质量为M的木块A从斜面底端开始以初速度v0上滑,然后又返回出发点,此时速度为v,且v<v0,在上述过程中斜面体一直静止不动,重力加速度大小为g. 关于上述运动过程的说法,错误的是( )
如图所示,斜面体B静置于水平桌面上,斜面上各处粗糙程度相同.一质量为M的木块A从斜面底端开始以初速度v0上滑,然后又返回出发点,此时速度为v,且v<v0,在上述过程中斜面体一直静止不动,重力加速度大小为g. 关于上述运动过程的说法,错误的是( )| A. | 物体上升的最大高度是$\frac{({{v}_{0}}^{2}+{v}^{2})}{4g}$ | |
| B. | 桌面对B的静摩擦力的方向先向右后向左 | |
| C. | A、B间因摩擦而放出的热量是$\frac{m{{v}_{0}}^{2}}{2}$ | |
| D. | 桌面对B的支持力大小,上滑过程中比下滑时小 |
4.下列各组物理量中,由电场自身性质决定的是( )
| A. | 电场力、电场强度 | B. | 电场强度、电势差 | ||
| C. | 电场力做的功、电势能 | D. | 电势差、电势能 |
9.关于感应电流,下列说法中正确的是( )
| A. | 只要穿过线圈的磁通量发生变化,线圈中就一定有感应电流 | |
| B. | 只要闭合导线做切割磁感线运动,导线中就一定有感应电流 | |
| C. | 穿过某闭合线圈的磁通量为零时,线圈电路中一定没有感应电流 | |
| D. | 当穿过闭合电路的磁通量发生变化时,闭合电路中一定有感应电流 |
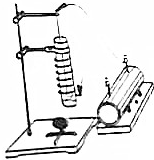 在玻璃管中心轴上安装一根指导线,玻璃管外绕有线圈,直导线的一端和线圈的一端分别跟感应圈的两放电柱相连,开始,感应圈未接通电源,点燃蚊香,让烟通过玻璃管冒出,当感应圈电源接通时,玻璃管中的导线和管外线圈间就会加上高电压,立即可以看到,不再有烟从玻璃管中冒出来了.过一会儿还可以看到管壁吸附了一层烟尘,请思考一下:这是什么原因?
在玻璃管中心轴上安装一根指导线,玻璃管外绕有线圈,直导线的一端和线圈的一端分别跟感应圈的两放电柱相连,开始,感应圈未接通电源,点燃蚊香,让烟通过玻璃管冒出,当感应圈电源接通时,玻璃管中的导线和管外线圈间就会加上高电压,立即可以看到,不再有烟从玻璃管中冒出来了.过一会儿还可以看到管壁吸附了一层烟尘,请思考一下:这是什么原因?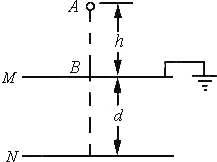 如图所示,两块水平放置的平行金属板M、N相距为d,组成一个电容为C的平行板电容器,M板接地,M板接地,板正中央有一小孔B,从B孔正上方的h处的A点,一滴一滴地由静止滴下质量为m、电荷量为q的带电油滴,油滴穿过B孔后落到N板,把全部电荷量传给N板,若不计空气阻力及板外电场,问:
如图所示,两块水平放置的平行金属板M、N相距为d,组成一个电容为C的平行板电容器,M板接地,M板接地,板正中央有一小孔B,从B孔正上方的h处的A点,一滴一滴地由静止滴下质量为m、电荷量为q的带电油滴,油滴穿过B孔后落到N板,把全部电荷量传给N板,若不计空气阻力及板外电场,问: