题目内容
8.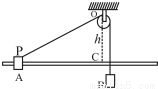 如图所示,水平光滑长杆上套有小物块A,细线跨过位于O点的轻质光滑定滑轮,一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为O点正下方杆上的点,滑轮到杆的距离OC=h.开始时A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.则下列说法正确的是( )
如图所示,水平光滑长杆上套有小物块A,细线跨过位于O点的轻质光滑定滑轮,一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为O点正下方杆上的点,滑轮到杆的距离OC=h.开始时A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.则下列说法正确的是( )| A. | 物块A由P点出发第一次到达C点过程中,速度先增大后减小 | |
| B. | 物块A由P点出发第一次到达C点过程中,细线对A拉力的功率一直增大 | |
| C. | 物块A经过C点时的速度大小为$\sqrt{2gh}$ | |
| D. | 在物块A由P点出发第一次到达C点过程中,细线对物块B的拉力先小于B的重力后大于B的重力 |
分析 在绳子作用下,物块从A到C的过程中,A一直加速,而B先加速后减速,根据B的加速度方向,分析细线的拉力和其重力的大小关系.根据P=Fvcosα分析细线对A拉力的功率如何变化.A到达C时,B的速度为零,根据系统的机械能守恒求物块A经过C点时的速度.
解答 解:A、物块A由P点出发第一次到达C点过程中,物块B从释放到了最低点,绳子的拉力对A一直做正功,其动能一直增大,速度一直增大,故A错误.
B、根据功率公式P=Fvcosα知,在P点,物块A的速度为零,细线对A拉力的功率为零.在C点,拉力和速度垂直,细线对A拉力的功率也为零,所以物块A由P点出发第一次到达C点过程中,细线对A拉力的功率先增大后减小,故B错误.
C、物块A经过C点时B的速度为0,根据系统的机械能守恒得:mBg($\frac{h}{sin30°}$-h)=$\frac{1}{2}$mAvA2,又 mB=mA,解得:vA=$\sqrt{2gh}$.故C正确.
D、物块A经过C点时B的速度为0,可知在物块A由P点出发第一次到达C点过程中,B的速度先增大后减小,加速度先向下后向上,B先处于失重状态后处于超重状态,所以细线对物块B的拉力先小于B的重力后大于B的重力,故D正确.
故选:CD
点评 本题是系统的机械能守恒问题,关键要抓住两个物体的速度关系,知道物块A经过C点时B的速度为0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18. 如图所示,在光滑水平桌面上有一质量为1kg的木块A,其左右两侧与轻弹簧相连,弹簧另一端都通过轻绳跨过定滑轮挂着两个质量均为0.5kg的钩码,滑轮摩擦不计,两钩码间用轻绳相连,系统处于静止状态.现将右侧两钩码间的绳子剪断,在剪断绳的瞬间,下列说法正确的是(取g=10m/s2)( )
如图所示,在光滑水平桌面上有一质量为1kg的木块A,其左右两侧与轻弹簧相连,弹簧另一端都通过轻绳跨过定滑轮挂着两个质量均为0.5kg的钩码,滑轮摩擦不计,两钩码间用轻绳相连,系统处于静止状态.现将右侧两钩码间的绳子剪断,在剪断绳的瞬间,下列说法正确的是(取g=10m/s2)( )
 如图所示,在光滑水平桌面上有一质量为1kg的木块A,其左右两侧与轻弹簧相连,弹簧另一端都通过轻绳跨过定滑轮挂着两个质量均为0.5kg的钩码,滑轮摩擦不计,两钩码间用轻绳相连,系统处于静止状态.现将右侧两钩码间的绳子剪断,在剪断绳的瞬间,下列说法正确的是(取g=10m/s2)( )
如图所示,在光滑水平桌面上有一质量为1kg的木块A,其左右两侧与轻弹簧相连,弹簧另一端都通过轻绳跨过定滑轮挂着两个质量均为0.5kg的钩码,滑轮摩擦不计,两钩码间用轻绳相连,系统处于静止状态.现将右侧两钩码间的绳子剪断,在剪断绳的瞬间,下列说法正确的是(取g=10m/s2)( )| A. | 左侧两钩码的加速度大小为2m/s2,方向竖直向下 | |
| B. | 右侧上方钩码的加速度大小为10m/s2,方向竖直向上 | |
| C. | 物块A的加速度大小为5m/s2,方向水平向左 | |
| D. | 右侧下方钩码的加速度为零 |
16. 如图所示,ABCD为正方形,带电粒子从AD边中点0以速度v垂直AD边射入,当正方形内存在垂直纸面的匀强磁场时,粒子从C点射出磁场,当正方形内存在平行AD边的匀强电场时,粒子也从C点射出,取sin37°=0.6,cos37°=O.8,则( )
如图所示,ABCD为正方形,带电粒子从AD边中点0以速度v垂直AD边射入,当正方形内存在垂直纸面的匀强磁场时,粒子从C点射出磁场,当正方形内存在平行AD边的匀强电场时,粒子也从C点射出,取sin37°=0.6,cos37°=O.8,则( )
 如图所示,ABCD为正方形,带电粒子从AD边中点0以速度v垂直AD边射入,当正方形内存在垂直纸面的匀强磁场时,粒子从C点射出磁场,当正方形内存在平行AD边的匀强电场时,粒子也从C点射出,取sin37°=0.6,cos37°=O.8,则( )
如图所示,ABCD为正方形,带电粒子从AD边中点0以速度v垂直AD边射入,当正方形内存在垂直纸面的匀强磁场时,粒子从C点射出磁场,当正方形内存在平行AD边的匀强电场时,粒子也从C点射出,取sin37°=0.6,cos37°=O.8,则( )| A. | 电场强度与磁感应强度的比值为1.25v | |
| B. | 电场强度与磁感应强度的比值为0.8v | |
| C. | 粒子在磁场中运动的时间与电场中运动的时间比为$\frac{53π}{144}$ | |
| D. | 粒子在磁场中运动的时间与电场中运动的时间比为$\frac{37π}{144}$ |
3. 如图所示是一理想的自耦变压器,A、B端接交流电源,C、D端接负载电阻R,P为滑动触头,当P逆时针转动时,下列结论正确的是( )
如图所示是一理想的自耦变压器,A、B端接交流电源,C、D端接负载电阻R,P为滑动触头,当P逆时针转动时,下列结论正确的是( )
 如图所示是一理想的自耦变压器,A、B端接交流电源,C、D端接负载电阻R,P为滑动触头,当P逆时针转动时,下列结论正确的是( )
如图所示是一理想的自耦变压器,A、B端接交流电源,C、D端接负载电阻R,P为滑动触头,当P逆时针转动时,下列结论正确的是( )| A. | R两端的电压下降,电流减小 | B. | R两端的电压升高,电流增大 | ||
| C. | R两端的电压升高,电流减小 | D. | R消耗的功率不变 |
17.下列关于质点的说法中正确的是( )
| A. | 质量很大的物体不可以看作质点 | |
| B. | 只有体积很小的物体才能看作质点 | |
| C. | 研究地球绕太阳公转时可以将地球看作质点 | |
| D. | 研究某学生骑车姿势的变化时可以把学生和车看作质点 |
 在匀强磁场中有一个原来静止的碳14原子核发生了某种衰变,放出一个带电粒子并形成一个新的反冲核,已知放射出的粒子速度方向及反冲核的速度方向均与磁场方向垂直,它们在磁场中运动的径迹是两个相内切的圆,如图所示,两圆的直径之比为7:1,则可以判断,粒子与反冲核的电性相反(填“相同”或“相反”),粒子与反冲核的电荷量之比为1:7,粒子与反冲核的动量大小之比为1:1.
在匀强磁场中有一个原来静止的碳14原子核发生了某种衰变,放出一个带电粒子并形成一个新的反冲核,已知放射出的粒子速度方向及反冲核的速度方向均与磁场方向垂直,它们在磁场中运动的径迹是两个相内切的圆,如图所示,两圆的直径之比为7:1,则可以判断,粒子与反冲核的电性相反(填“相同”或“相反”),粒子与反冲核的电荷量之比为1:7,粒子与反冲核的动量大小之比为1:1.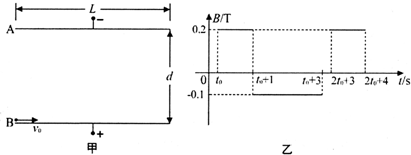
 如图所示,质量m=2kg的物体静止于水平地面的A处,A、B间距L=20m.用大小为30N,沿水平方向的外力拉此物体,经t0=2s拉至B处.(取g=10m/s2) 求:
如图所示,质量m=2kg的物体静止于水平地面的A处,A、B间距L=20m.用大小为30N,沿水平方向的外力拉此物体,经t0=2s拉至B处.(取g=10m/s2) 求: 某学校组织两千余名同学在运动场开展阳光体育活动,某兴趣小组的同学在水平面上用三脚架固定相机抓拍,相机的质量为M,三脚架的三根轻质支架等长,与竖直方向均成α角,求每根支架承受的压力大小.
某学校组织两千余名同学在运动场开展阳光体育活动,某兴趣小组的同学在水平面上用三脚架固定相机抓拍,相机的质量为M,三脚架的三根轻质支架等长,与竖直方向均成α角,求每根支架承受的压力大小.