题目内容
如图a所示,一轻绳上端系在车的左上角A点,另一轻绳一端系在车左壁上B点.B点在A点正下方,AB距离为L,两绳另一端在c点相结并系一质量为m的小球,绳AC长为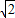 L,BC长为L,两绳能够承受的最大拉力均为2mg,则(1)绳BC刚好被拉直时(如图b),车的加速度大小为 g;(2)为不拉断轻绳,车的最大加速度大小为 g.
L,BC长为L,两绳能够承受的最大拉力均为2mg,则(1)绳BC刚好被拉直时(如图b),车的加速度大小为 g;(2)为不拉断轻绳,车的最大加速度大小为 g.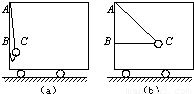
【答案】分析:(1)当BC绳刚好被拉直时,小球受AC绳的拉力和重力,根据牛顿第二定律,运用合成法求出球的加速度,抓住车和球的加速度相等得出车的加速度.
(2)抓住小球竖直方向上受力平衡求出AC绳的拉力,当BC拉力达到最大时,车的加速度最大.根据牛顿第二定律求出车的最大加速度.
解答: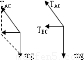 解:(1)绳BC刚好被拉直时(如图b),小球受重力、AC绳的拉力时,它们的合力水平向左,根据牛顿第二定律有:mgtan45°=ma,解得a=g.
解:(1)绳BC刚好被拉直时(如图b),小球受重力、AC绳的拉力时,它们的合力水平向左,根据牛顿第二定律有:mgtan45°=ma,解得a=g.
(2)小球在竖直方向上平衡,有:TACsin45°=mg,
解得TAC=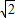 mg,且保持不变,
mg,且保持不变,
知BC绳达到最大拉力时,加速度最大.
根据牛顿第二定律得,TACcos45°+TBC=mam
解得am=3g.
故答案为:1,3
点评:解决本题的关键能够正确地受力分析,会运用合成法和正交分解,并结合牛顿第二定律进行求解.
(2)抓住小球竖直方向上受力平衡求出AC绳的拉力,当BC拉力达到最大时,车的加速度最大.根据牛顿第二定律求出车的最大加速度.
解答:
 解:(1)绳BC刚好被拉直时(如图b),小球受重力、AC绳的拉力时,它们的合力水平向左,根据牛顿第二定律有:mgtan45°=ma,解得a=g.
解:(1)绳BC刚好被拉直时(如图b),小球受重力、AC绳的拉力时,它们的合力水平向左,根据牛顿第二定律有:mgtan45°=ma,解得a=g.(2)小球在竖直方向上平衡,有:TACsin45°=mg,
解得TAC=
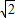 mg,且保持不变,
mg,且保持不变,知BC绳达到最大拉力时,加速度最大.
根据牛顿第二定律得,TACcos45°+TBC=mam
解得am=3g.
故答案为:1,3
点评:解决本题的关键能够正确地受力分析,会运用合成法和正交分解,并结合牛顿第二定律进行求解.

练习册系列答案
相关题目
 如图a所示,一轻绳上端系在车的左上角A点,另一轻绳一端系在车左壁上B点.B点在A点正下方,AB距离为L,两绳另一端在c点相结并系一质量为m的小球,绳AC长为
如图a所示,一轻绳上端系在车的左上角A点,另一轻绳一端系在车左壁上B点.B点在A点正下方,AB距离为L,两绳另一端在c点相结并系一质量为m的小球,绳AC长为 (2008?徐汇区模拟)如图a所示,一轻绳上端系在车的左上角A点,另一轻绳一端系在车左壁上B点.B点在A点正下方,AB距离为L,两绳另一端在c点相结并系一质量为m的小球,绳AC长为
(2008?徐汇区模拟)如图a所示,一轻绳上端系在车的左上角A点,另一轻绳一端系在车左壁上B点.B点在A点正下方,AB距离为L,两绳另一端在c点相结并系一质量为m的小球,绳AC长为 如图a所示,一轻绳上端系在车的左上角A点,另一轻绳一端系在车左壁上B点.B点在A点正下方,AB距离为L,两绳另一端在c点相结并系一质量为m的小球,绳AC长为
如图a所示,一轻绳上端系在车的左上角A点,另一轻绳一端系在车左壁上B点.B点在A点正下方,AB距离为L,两绳另一端在c点相结并系一质量为m的小球,绳AC长为 L,BC长为L,两绳能够承受的最大拉力均为2mg,则(1)绳BC刚好被拉直时(如图b),车的加速度大小为______;(2)为不拉断轻绳,车的最大加速度大小为______.
L,BC长为L,两绳能够承受的最大拉力均为2mg,则(1)绳BC刚好被拉直时(如图b),车的加速度大小为______;(2)为不拉断轻绳,车的最大加速度大小为______.
