��Ŀ����
�����ֱ�Ϊm1��m2������С������������ӣ�m1=4m0��m2=5m0�������λ����Ǧ�=37��Ĺ⻬б�涥�˵��Ử�֣�������ת����Ħ�����ƣ�б��̶���ˮƽ�����ϣ���ͼ��ʾ��m1���գ�m2����б���ϣ�m2��б����ɾ�ֹ��ʼ�˶���б�涥�ˣ���ʱΪt����֪�������ٶ�Ϊg��sin37��=0.6��cos37��=0.8����
��1����m1��m2λ�û�����ʹm2���գ�m1����б���ϣ�m1��б����ɾ�ֹ��ʼ�˶���б�涥�ˣ�������������֮�ȣ�
��2����m1���գ�m2����б���ϣ�����m2��������ʹm2��б�涥���ɾ�ֹ��ʼ�˶���б��˵�ʱ��ҲΪt��m2���ӵ�������
��1����m1��m2λ�û�����ʹm2���գ�m1����б���ϣ�m1��б����ɾ�ֹ��ʼ�˶���б�涥�ˣ�������������֮�ȣ�
��2����m1���գ�m2����б���ϣ�����m2��������ʹm2��б�涥���ɾ�ֹ��ʼ�˶���б��˵�ʱ��ҲΪt��m2���ӵ�������

��1����һ�Σ�����m1��m1g-T1=m1a1��
����m2��T1-m2g?sin��=m2a1
���ԣ�
=
?T1=
�ڶ��Σ�����m2��m2g-T2=m2a2��
����m1��T2-m1g?sin��=m1a2��
���ԣ�
=
?T2=
��
���ԣ�
=1��
��2����һ�Σ�����m1��m1g-T1=m1a1
����m2��T1-m2g?sin��=m2a1��
���ԣ�a1=
��
����m2����������m2��m2��g?sin��-T3=m2��a3��
����m1��T3-m1g=m1a3��
���ԣ�a3=
���ݣ�S=
at2���ɵã�
a1=a3?
=
?m2��=
mo��
��m=m2��-m2=
mo��
�𣺣�1��������������֮��1��1��2��m2���ӵ�����Ϊ
m0
����m2��T1-m2g?sin��=m2a1
���ԣ�
| m1g-T1 |
| T1-m2g?sin�� |
| m1 |
| m2 |
| m1m2g+m1m2g?sin�� |
| m1+m2 |
�ڶ��Σ�����m2��m2g-T2=m2a2��
����m1��T2-m1g?sin��=m1a2��
���ԣ�
| m2g-T2 |
| T2-m1g?sin�� |
| m2 |
| m1 |
| m1m2g+m1m2g?sin�� |
| m1+m2 |
���ԣ�
| T1 |
| T2 |
��2����һ�Σ�����m1��m1g-T1=m1a1
����m2��T1-m2g?sin��=m2a1��
���ԣ�a1=
| m1g-m2g?sin�� |
| m1+m2 |
����m2����������m2��m2��g?sin��-T3=m2��a3��
����m1��T3-m1g=m1a3��
���ԣ�a3=
| m2��g?sin��-m1g |
| m1+m2�� |
���ݣ�S=
| 1 |
| 2 |
a1=a3?
| m1g-m2g?sin�� |
| m1+m2 |
| m2��g?sin��-m1g |
| m2��+m1 |
| 100 |
| 11 |
��m=m2��-m2=
| 45 |
| 11 |
�𣺣�1��������������֮��1��1��2��m2���ӵ�����Ϊ
| 45 |
| 11 |

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
�������ǵ������ֱ�Ϊm1��m2����̫�����еĹ���볤��ֱ�Ϊr1��r2�������ǵĹ�ת����֮��Ϊ��������
A��
| ||||||||
B��
| ||||||||
C��
| ||||||||
| D����ȷ�� |
 һ��˫�ǣ��������L�������ֱ�ΪM1��M2���������幹�ɣ����Ǽ������ܴ���δ������һ������Ϊ������������ij��ΪԲ����Բ���˶��Ľ������ͼ��ʾ���������Ǹ�����ת�뾶�ͽ��ٶȸ��Ƕ��٣�
һ��˫�ǣ��������L�������ֱ�ΪM1��M2���������幹�ɣ����Ǽ������ܴ���δ������һ������Ϊ������������ij��ΪԲ����Բ���˶��Ľ������ͼ��ʾ���������Ǹ�����ת�뾶�ͽ��ٶȸ��Ƕ��٣� ��ͼ��ʾ��ˮƽ���õĽ���ƽ�а��B��ӵأ�A�����Ϊ+U����������Ϊd��d�������ijߴ�С�ܶ࣬������֮����һ��Ϊl�ľ�Ե��ˣ����ƹ̶���O����ֱ������Ħ��������ת�����˵����˷ֱ���������С��1��2�����ǵ������ֱ�Ϊm1��m2��m1��m2�����ǵĴ������ֱ�Ϊ-q1��+q2��q1��q2��������ͼʾˮƽλ�ôӾ�ֹ��ʼת����ֱλ��ʱ��������
��ͼ��ʾ��ˮƽ���õĽ���ƽ�а��B��ӵأ�A�����Ϊ+U����������Ϊd��d�������ijߴ�С�ܶ࣬������֮����һ��Ϊl�ľ�Ե��ˣ����ƹ̶���O����ֱ������Ħ��������ת�����˵����˷ֱ���������С��1��2�����ǵ������ֱ�Ϊm1��m2��m1��m2�����ǵĴ������ֱ�Ϊ-q1��+q2��q1��q2��������ͼʾˮƽλ�ôӾ�ֹ��ʼת����ֱλ��ʱ��������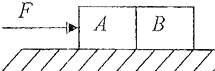 ��ͼ��ʾ�������ֱ�Ϊm1��m2��A��B����������ڴֲ�ˮƽ�����ϣ�����F������A�����ϣ�������˵����ȷ���ǣ�������
��ͼ��ʾ�������ֱ�Ϊm1��m2��A��B����������ڴֲ�ˮƽ�����ϣ�����F������A�����ϣ�������˵����ȷ���ǣ�������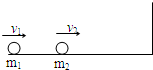 ��1����3-5������ķ��ֵ��Ӻ���ԭ����������ɵķֲ������⣬��ѧ�������������ģ�ͣ���������϶���ռԭ���������ֵ�����ɼ����ں�С�Ŀռ䷶Χ�ڣ��������������ת����ģ�ͳ�ԭ�ӵ��к�ģ�ͣ��������ԭ���к�ģ�͵Ŀ�ѧ����
��1����3-5������ķ��ֵ��Ӻ���ԭ����������ɵķֲ������⣬��ѧ�������������ģ�ͣ���������϶���ռԭ���������ֵ�����ɼ����ں�С�Ŀռ䷶Χ�ڣ��������������ת����ģ�ͳ�ԭ�ӵ��к�ģ�ͣ��������ԭ���к�ģ�͵Ŀ�ѧ����