题目内容
10．如图所示，矩形线框以恒定速度v通过匀强有界磁场，则在整个过程中，以下说法正确的是（ ）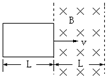
| A． | 线框中的感应电流方向是先逆时针方向，后顺时针方向 | |
| B． | 线框中的感应电流方向是先顺时针方向，后逆时针方向 | |
| C． | 线框中的感应电流的方向一直是逆时针方向 | |
| D． | 线框离开磁场过程中所受安培力方向向右 |
分析 根据楞次定律判断出线框中的感应电流的方向，由左手定则判断线框所受的安培力的方向．
解答 解：ABC、线圈进入磁场时，磁通量增大，根据楞次定律知，线圈中的感应电流方向为逆时针方向．线圈出磁场时，磁通量减小，根据楞次定律知，感应电流的方向为顺时针方向．故A正确，BC错误．
D、进入磁场时，根据左手定则，右边所受的安培力方向向左．出磁场时，根据左手定则，线框左边所受的安培力方向向左．故D错误．
故选：A．
点评 解决本题的关键掌握楞次定则判断感应电流的方向，会根据左手定则判断安培力的方向．本题判断线框的受力分析，也可以根据楞次定律的另一种表述判断，即感应电流产生的效果，阻碍线圈的运动．
练习册系列答案
相关题目
20．
如图所示，劲度系数为k的轻弹簧下端系一个质量为m的小球A，小球被水平挡板P托住使弹簧长度恰为自然长度（小球与挡板不粘连），然后使挡板P以恒定的加速度a（a＜g）竖直向下做匀加速直线运动，对小球从开始运动直至到达最低点的过程，用t表示与挡板分离所经历的时间，用x表示小球速度最大时弹簧的伸长量，则（ ）
如图所示，劲度系数为k的轻弹簧下端系一个质量为m的小球A，小球被水平挡板P托住使弹簧长度恰为自然长度（小球与挡板不粘连），然后使挡板P以恒定的加速度a（a＜g）竖直向下做匀加速直线运动，对小球从开始运动直至到达最低点的过程，用t表示与挡板分离所经历的时间，用x表示小球速度最大时弹簧的伸长量，则（ ）| A． | t=$\sqrt{\frac{2m（g-a）}{ka}}$ | B． | t=$\sqrt{\frac{2mg}{ka}}$ | C． | x=0 | D． | x=$\frac{mg}{k}$ |
1．一个按正弦规律变化的交变电流的图象如图所示，由图可知（ ）
| A． | 该交变电流的最小值为-20A | |
| B． | 该交变电流的有效值为14.1 A | |
| C． | 该交变电流的瞬时值表达式为i=20sin0.02t（A） | |
| D． | 该交变电流的频率为0.2 Hz |
18．
如图所示，高为h=1.25m的平台上，覆盖着一层薄冰．现有一质量为60kg的滑雪爱好者，以一定的初速度v向平台边缘滑去，着地时的速度方向与水平地面的夹角为45°（重力加速度g取10m/s2）．由此可知以下判断错误的是（ ）
如图所示，高为h=1.25m的平台上，覆盖着一层薄冰．现有一质量为60kg的滑雪爱好者，以一定的初速度v向平台边缘滑去，着地时的速度方向与水平地面的夹角为45°（重力加速度g取10m/s2）．由此可知以下判断错误的是（ ）| A． | 滑雪者离开平台边缘时的速度大小是5.0m/s | |
| B． | 滑雪者着地点到平台边缘的水平距离是2.5m | |
| C． | 滑雪者在空中运动的时间为0.5s | |
| D． | 着地时滑雪者的瞬时速度为5m/s |
如图，在水平面上有一个固定的两根光滑金属杆制成的37°角的导轨AO和BO，在导轨上放置一根始终和OB垂直的金属杆CD，导轨和金属杆是用同种材料制成的，单位长度的电阻值均为0.1Ω/m，整个装置位于垂直纸面向里的匀强磁场中，匀强磁场的磁感应强度B=0.2T，现给棒CD一个水平向右的外力，使CD棒从t=0时刻由O点处开始向右做匀加速直线运动，加速度大小为1m/s2，
19．
实验题
某同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关，他以圆型砂轮为研究对象，研究其转动动能与其质量、半径、角速度等的具体关系．如图所示，砂轮由动力带动匀速旋转，测得其角速度为ω，然后让砂轮脱离动力，用一把弹性尺子与砂轮接触使砂轮慢慢停下，设尺和砂轮间的摩擦力恒为$\frac{10}{π}$N，不计转轴的质量及其与支架间的摩擦．分别取不同质量、不同半径的砂轮，使其以不同的角速度旋转进行实验，最后得到的数据如表所示：
①由1至3次的实验数据可得砂轮的转动动能与角速度的关系为B（选填字母符号）
A． Ek∞ω B．Ek∞ω2 C．Ek∞ω3
②由4次和6次的实验数据可计算出第5次砂轮的转动动能，A=19.2J
③由7至9次的实验数据可得砂轮的转动动能与砂轮半径的关系为B（选填字母符号）
A．Ek∞r B．Ek∞r2 C．Ek∞r3．
实验题某同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关，他以圆型砂轮为研究对象，研究其转动动能与其质量、半径、角速度等的具体关系．如图所示，砂轮由动力带动匀速旋转，测得其角速度为ω，然后让砂轮脱离动力，用一把弹性尺子与砂轮接触使砂轮慢慢停下，设尺和砂轮间的摩擦力恒为$\frac{10}{π}$N，不计转轴的质量及其与支架间的摩擦．分别取不同质量、不同半径的砂轮，使其以不同的角速度旋转进行实验，最后得到的数据如表所示：
| 次数 | 半径/cm | 质量/m0 | 角速度/rad•s-1 | 圈数 | 转动动能/J |
| 1 | 4 | 1 | 2 | 8 | 6.4 |
| 2 | 4 | 1 | 3 | 18 | 14.4 |
| 3 | 4 | 1 | 4 | 32 | 25.6 |
| 4 | 4 | 2 | 2 | 16 | 12.8 |
| 5 | 4 | 3 | 2 | 24 | A |
| 6 | 4 | 4 | 2 | 32 | 25.6 |
| 7 | 8 | 1 | 2 | 16 | 25.6 |
| 8 | 12 | 1 | 2 | 24 | 57.6 |
| 9 | 16 | 1 | 2 | 32 | 102.4 |
A． Ek∞ω B．Ek∞ω2 C．Ek∞ω3
②由4次和6次的实验数据可计算出第5次砂轮的转动动能，A=19.2J
③由7至9次的实验数据可得砂轮的转动动能与砂轮半径的关系为B（选填字母符号）
A．Ek∞r B．Ek∞r2 C．Ek∞r3．
20．
如图所示，A、B两物体彼此接触静止于光滑的水平桌面上，物体A的上表面是半径为R的光滑圆形轨道，物体C由静止开始从A上圆形轨道的右侧最高点下滑，则有（ ）
如图所示，A、B两物体彼此接触静止于光滑的水平桌面上，物体A的上表面是半径为R的光滑圆形轨道，物体C由静止开始从A上圆形轨道的右侧最高点下滑，则有（ ）| A． | A和B不会出现分离现象 | |
| B． | 当C第一次滑到圆弧最低点时，A和B开始分离 | |
| C． | A将会在桌面左边滑出 | |
| D． | A不会在桌面上滑出 |