题目内容
【题目】如图所示，直角三棱镜置于空气中，已知∠A=60°，∠C=90°，一束极细单色光从AC的中点D垂直AC面入射，AD= 
m，棱镜对该单色光的折射率n= 
，求：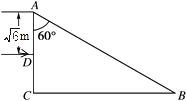
（1）光从棱镜第一次射入空气时的折射角；
（2）光从进入棱镜到第一次射入空气所经历的时间（已知光在真空中的传播速度为c=3×108m/s，结果保留一位有效数字）．
【答案】
（1）
解：设玻璃对空气的临界角为C，
则：sinC= 
= 
代入数值得：C=45°
由几何知识得 i1=60°＞45°，所以光线在AB面上将发生全反射
i2=30°＜C，则光线从BC面上第一次射入空气．
由折射定律有： 
=n
代入数值得：折射角 r=45°
（2）
解：棱镜中光速为：v= 
则光从进入棱镜到第一次射入空气所经历的时间：t= 
AD+ 
=3×10﹣8s
【解析】（1）画出光路图，由几何知识找出角度关系，确定出光线到达AB面时的入射角，与临界角比较，判断能否发生全反射．再运用同样的思路分析光线在AC面上能否发生全反射，若不发生全反射，光线将从棱镜第一次射入空气，由折射定律求解折射角．（2）由v= 求出光在棱镜中的传播速度，运用几何知识求出光棱镜中传播的距离，由运动学知识可以求解时间．
【考点精析】通过灵活运用光的折射，掌握光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射即可以解答此题．
练习册系列答案
相关题目
