题目内容
某实验小组为了测试玩具小车的加速性能,设置了如图所示的轨道.轨道由半径为R=0.2m的光滑的圆弧轨道和动摩擦因数为μ=0.4的粗糙部分组成.现将小车从轨道上的A点开始以恒定的功率启动,经5秒后由于技术故障动力消失.小车滑过圆弧轨道从C点飞出落到水平面上的D点.实验测得小车的质量m=0.4Kg,AB间距离L=8m,BD间距离为0.4m,重力加速度g=10m/s2.求:(1)小车从C点飞出时的速度?
(2)小车滑过B点时对轨道B点的压力?
(3)小车电动机的输出功率P.

【答案】分析:(1)小车从C点飞出时做平抛运动,运用运动的分解方法,结合平抛运动的规律即可求出小车从C点飞出时的速度.
(2)小车由B运动到C点,轨道的支持力不做功,只有重力对小车做功,其机械能守恒,即可由机械能守恒定律求出小车经过B点时的速度大小.在B点,由重力和轨道对小车的支持力的合力充当向心力,由牛顿第二定律求得轨道对小车的支持力,再由牛顿第三定律得到小车对轨道的压力.
(3)小车A点运动到B点的过程,牵引力对小车做功为Pt,摩擦力做功为-μmgL,根据动能定理求解P.
解答:解:(1)小车从C点飞出时做平抛运动,设落地时间为t,则有:
2R= gt2
gt2
xBD=vct
解得:vc= m/s
m/s
(2)小车由B运动到C点,机械能守恒,则有;
mg?2R+ mvc2=
mvc2= mvB2
mvB2
由牛顿第二定律得:
FN-mg=m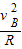
解得:FN=24N
由牛顿第三定律得小车滑过B点时对轨道B点的压力大小为24N,方向竖直向下.
(3)小车A点运动到B点的过程,由动能定理得
Pt-μmgL= mvB2
mvB2
解得 P=2.96W
答:
(1)小车从C点飞出时的速度为 m/s.
m/s.
(2)小车滑过B点时对轨道B点的压力为24N,方向竖直向下.
(3)小车电动机的输出功率P为2.96W.
点评:本题有三个运动过程,把握各个过程的物理规律是解题的关键和根本.
(2)小车由B运动到C点,轨道的支持力不做功,只有重力对小车做功,其机械能守恒,即可由机械能守恒定律求出小车经过B点时的速度大小.在B点,由重力和轨道对小车的支持力的合力充当向心力,由牛顿第二定律求得轨道对小车的支持力,再由牛顿第三定律得到小车对轨道的压力.
(3)小车A点运动到B点的过程,牵引力对小车做功为Pt,摩擦力做功为-μmgL,根据动能定理求解P.
解答:解:(1)小车从C点飞出时做平抛运动,设落地时间为t,则有:
2R=
 gt2
gt2xBD=vct
解得:vc=
 m/s
m/s(2)小车由B运动到C点,机械能守恒,则有;
mg?2R+
 mvc2=
mvc2= mvB2
mvB2 由牛顿第二定律得:
FN-mg=m
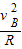
解得:FN=24N
由牛顿第三定律得小车滑过B点时对轨道B点的压力大小为24N,方向竖直向下.
(3)小车A点运动到B点的过程,由动能定理得
Pt-μmgL=
 mvB2
mvB2 解得 P=2.96W
答:
(1)小车从C点飞出时的速度为
 m/s.
m/s.(2)小车滑过B点时对轨道B点的压力为24N,方向竖直向下.
(3)小车电动机的输出功率P为2.96W.
点评:本题有三个运动过程,把握各个过程的物理规律是解题的关键和根本.

练习册系列答案
相关题目
 某实验小组为了测试玩具小车的加速性能,设置了如图所示的轨道.轨道由半径为R=0.2m的光滑的圆弧轨道和动摩擦因数为μ=0.4的粗糙部分组成.现将小车从轨道上的A点开始以恒定的功率启动,经5秒后由于技术故障动力消失.小车滑过圆弧轨道从C点飞出落到水平面上的D点.实验测得小车的质量m=0.4Kg,AB间距离L=8m,BD间距离为0.4m,重力加速度g=10m/s2.求:
某实验小组为了测试玩具小车的加速性能,设置了如图所示的轨道.轨道由半径为R=0.2m的光滑的圆弧轨道和动摩擦因数为μ=0.4的粗糙部分组成.现将小车从轨道上的A点开始以恒定的功率启动,经5秒后由于技术故障动力消失.小车滑过圆弧轨道从C点飞出落到水平面上的D点.实验测得小车的质量m=0.4Kg,AB间距离L=8m,BD间距离为0.4m,重力加速度g=10m/s2.求:

