题目内容
7．
如图所示，表面粗糙的水平传送带匀速向右传动．现在其左侧的A处轻轻放上一物块，则该物块的运动情况和受力情况可能为（ ）| A． | 一直向右做匀加速运动 | |
| B． | 先向右做匀加速运动，后继续向右做匀速运动 | |
| C． | 先受到向右的滑动摩擦力，后受到向右的静摩擦力 | |
| D． | 先受到向右的滑动摩擦力，后不受摩擦力 |
分析 木块初速度为零，由静到动是加速，根据物体的加速长度及传送带的长度关系分析物体可能的运动情况．
解答 解：A、B、木块初速度为零，由静到动是加速，若达到最右端时仍未与传送带相对静止，则一直加速；故A正确；
B、若传送带足够长，故最后一起匀速，故先做加速运动，再做匀速运动；故B正确；
C、D、滑块向右加速阶段，加速度向右，故合力向右，静摩擦力向右；滑块匀速阶段，合力为零，故摩擦力为零，即不受摩擦力；故C错误，D正确；
故选：ABD．
点评 本题关键是明确求解摩擦力方向的思路，先确定运动情况，得到加速度情况和合力情况，最后得到摩擦力情况．
练习册系列答案
相关题目
三个质量相同，带相同正电荷的小球，从同一高度开始下落．其中甲直接落地，乙在下落过程中经过一个水平方向的匀强电场区，丙经过一个水平方向的匀强磁场区．如图所示，不计空气阻力，则落到同一水平地面上时，乙球的速度最大，丙球最后到达地面．
18．
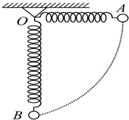如图所示，一轻弹簧固定于O点，另一端系一重物，将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放，让它自由摆下．不计空气阻力，在重物由A点摆向最低点B的过程中（ ）
如图所示，一轻弹簧固定于O点，另一端系一重物，将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放，让它自由摆下．不计空气阻力，在重物由A点摆向最低点B的过程中（ ）| A． | 重物的重力势能增加 | B． | 弹簧的弹性势能不变 | ||
| C． | 重物的机械能减少 | D． | 重物和弹簧组成的系统机械能减少 |
某同学利用电压表和电阻箱测定一种特殊电池的电动势，该同学利用如图所示的电路进行实验，图中R0为已知阻值的定值电阻．
在水平地面上有一个质量为4.0kg的物体，物体在水平拉力F的作用下由静止开始运动．10s后拉力大小减小为$\frac{1}{3}$F，并保持恒定．该物体的速度图象如图所示．求：
19．
质量为m的三角形木楔A置于倾角为θ的固定斜面上，它与斜面间的动摩擦因数为μ，一水平力F作用在木楔A的竖直平面上，在力F的推动下，木楔A沿斜面以恒定的加速度a向上滑动，则F的大小为（ ）
质量为m的三角形木楔A置于倾角为θ的固定斜面上，它与斜面间的动摩擦因数为μ，一水平力F作用在木楔A的竖直平面上，在力F的推动下，木楔A沿斜面以恒定的加速度a向上滑动，则F的大小为（ ）| A． | $\frac{m（a-gsinθ）}{cosθ+μsinθ}$ | B． | $\frac{m[a+g（sinθ+μcosθ）]}{cosθ-μsinθ}$ | ||
| C． | $\frac{m（a+μgcosθ）}{cosθ}$ | D． | $\frac{{m[{a+g（sinθ+μcosθ）}]}}{cosθ}$ |
16．一辆汽车以10m/s的速度沿平直公路匀速前进，因发现障碍物而须立即刹车，以2m/s2的加速度做匀减速运动，则刹车后2秒的距离为（ ）
| A． | 24m | B． | 25m | C． | 16m | D． | 4m |
