题目内容
17.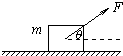 如图所示,在水平面上有一质量为m的物体,物体与水平面间的动摩擦因数为μ.
如图所示,在水平面上有一质量为m的物体,物体与水平面间的动摩擦因数为μ.(1)用一个大小不变的拉力F作用在物体上使物体沿水平面运动,拉力F与水平方向成夹角θ时,使物体产生加速度大小为多少?
(2)用一个大小不变的推力F作用在物体上使物体沿水平面运动,推力F与水平方程成夹角θ时,使物体产生加速度大小为多少?
分析 (1)对物体受力分析,受拉力、重力、支持力、摩擦力,根据牛顿第二定律列式求解即可;
(2)同样对物体受力分析,受拉力、重力、支持力、摩擦力,然后根据牛顿第二定律列式求解.
解答 解:(1)对物体受力分析,如图所示:
根据牛顿第二定律,有:
水平方向:Fcosθ-f=ma
竖直方向:N+Fsinθ-mg=0
其中:f=μN
联立解得:
a=$\frac{F(cosθ+μsinθ)}{m}-μg$
(2)对物体受力分析,受拉力、重力、支持力、摩擦力,然后根据牛顿第二定律,有:
水平方向:Fcosθ-f=ma
竖直方向:N-Fsinθ-mg=0
其中:f=μN
联立解得:
a=$\frac{F(cosθ-μsinθ)}{m}-μg$
答:(1)用一个大小不变的拉力F作用在物体上使物体沿水平面运动,拉力F与水平方向成夹角θ时,使物体产生加速度大小为$\frac{F(cosθ+μsinθ)}{m}-μg$;
(2)用一个大小不变的推力F作用在物体上使物体沿水平面运动,推力F与水平方程成夹角θ时,使物体产生加速度大小为$\frac{F(cosθ-μsinθ)}{m}-μg$.
点评 本题关键是明确物体的受力情况和运动情况,然后根据牛顿第二定律并结合正交分解法列式求解,基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图所示的电路中,输入电压恒为12V,灯泡L标有“6V,12w”的字样,电动机线圈的电阻RM=0.5Ω,若灯泡恰能正常发光,则下列说法中正确的是( )
如图所示的电路中,输入电压恒为12V,灯泡L标有“6V,12w”的字样,电动机线圈的电阻RM=0.5Ω,若灯泡恰能正常发光,则下列说法中正确的是( )
 如图所示的电路中,输入电压恒为12V,灯泡L标有“6V,12w”的字样,电动机线圈的电阻RM=0.5Ω,若灯泡恰能正常发光,则下列说法中正确的是( )
如图所示的电路中,输入电压恒为12V,灯泡L标有“6V,12w”的字样,电动机线圈的电阻RM=0.5Ω,若灯泡恰能正常发光,则下列说法中正确的是( )| A. | 电动机的输出功率为12W | B. | 电动机的输入功率是12W | ||
| C. | 电动机的热功率是2W | D. | 整个电路消耗的功率是22W |
5.将小球从地面以初速度V0竖直向上抛出,运动过程中小球受到的空气阻力大小不变,最终小球又回到地面,以地面为零势能面,则小球( )
| A. | 上升的最大高度小于$\frac{{V}_{0}^{2}}{2g}$ | |
| B. | 上升的时间大于下落的时间 | |
| C. | 上升过程中达到最大高度一半时其动能大于重力势能 | |
| D. | 下降过程中达到最大高度一半时其动能等于重力势能 |
2.某粒子的质量为m,带电量为q,它仅在静电力的作用下在电场中从A点运动到B点,速度由VA变为VB,则下列说法中正确的是( )
| A. | 该粒子的动能一定增加 | |
| B. | 该粒子的电势能一定增加 | |
| C. | 只有是匀强电场才可以求出A、B两点间的电势差 | |
| D. | 该粒子的动能可能始终不变 |
6.原来静止的两个物体,它们的质量之比为m1:m2=1:4.当合外力使它们获得相等的动能时,它们速度大小之比v1:v2等于( )
| A. | 1:4 | B. | 4:l | C. | 2:1 | D. | 1:2 |
7. 在如图所示的电路中,当开关S闭合后,水平放置的平行板电容器中有一带电液滴正好处于静止状态,现将开关S断开,则( )
在如图所示的电路中,当开关S闭合后,水平放置的平行板电容器中有一带电液滴正好处于静止状态,现将开关S断开,则( )
 在如图所示的电路中,当开关S闭合后,水平放置的平行板电容器中有一带电液滴正好处于静止状态,现将开关S断开,则( )
在如图所示的电路中,当开关S闭合后,水平放置的平行板电容器中有一带电液滴正好处于静止状态,现将开关S断开,则( )| A. | 液滴仍保持静止状态 | |
| B. | 液滴做自由落体运动 | |
| C. | 电容器上的带电荷量增大 | |
| D. | 电容器上的带电荷量与R1的大小有关 |
 如图所示,平行带电导体板A、B竖直放置,平行带电导体板C、D水平放置,B板上有一小孔,从小孔射出的带电粒子刚好可从C、D板间左上角切入C、D板间电场,已知C、D板间距离为d,长为2d,UAB=UCD=U>O,在C、D板右侧存在一个垂直纸面向内的只有左边界的水平匀强磁场.质量为m,电量为q的带正电粒子由静止从A板释放,沿直线运动至B板小孔后贴近C板进入G、D板间,最后能进入磁场中.(带电粒子的重力不计.)求:
如图所示,平行带电导体板A、B竖直放置,平行带电导体板C、D水平放置,B板上有一小孔,从小孔射出的带电粒子刚好可从C、D板间左上角切入C、D板间电场,已知C、D板间距离为d,长为2d,UAB=UCD=U>O,在C、D板右侧存在一个垂直纸面向内的只有左边界的水平匀强磁场.质量为m,电量为q的带正电粒子由静止从A板释放,沿直线运动至B板小孔后贴近C板进入G、D板间,最后能进入磁场中.(带电粒子的重力不计.)求: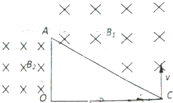 有一直角三角形OAC,OC长为12cm,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度B1=1T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度大小B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从C点以垂直于OC的速度v进入磁场,恰好经A点到达O点,不计粒子重力,求:
有一直角三角形OAC,OC长为12cm,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度B1=1T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度大小B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从C点以垂直于OC的速度v进入磁场,恰好经A点到达O点,不计粒子重力,求: