题目内容
 如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是
如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是
- A.FN增大,Ff持续增大
- B.FN不变,Ff不变
- C.FN增大,Ff先减小后增大
- D.FN减小,Ff先增大后减小
C
分析:使物体A和斜面体B一起向左做加速运动,加速度水平向左,将加速度分解为沿斜面向下和垂直于斜面向上两个方向,根据牛顿第二定律得到支持力FN和摩擦力Ff的关系式进行分析.
解答:当加速度较小时,摩擦力Ff沿斜面向上.将加速度分解为沿斜面向下和垂直于斜面向上.根据牛顿第二定律得
FN-mgcosθ=masinθ,
mgsinθ-Ff=macosθ,
得到FN=mgcosθ+masinθ Ff=mgsinθ-macosθ
可知当a增大时,FN增大,Ff减小.
当加速度较大时,摩擦力Ff沿斜面向下.根据牛顿第二定律得
FN-mgcosθ=masinθ,
mgsinθ+Ff=macosθ,
得到FN-mgcosθ=masinθ,Ff=macosθ-mgsinθ
可知当a增大时,FN增大,Ff增大.故C正确.
故选C
点评:本题考查灵活运用正交分解处理物理问题的能力,采用的是分解加速度,不分解要求的力的方法,使解题过程简洁方便.
分析:使物体A和斜面体B一起向左做加速运动,加速度水平向左,将加速度分解为沿斜面向下和垂直于斜面向上两个方向,根据牛顿第二定律得到支持力FN和摩擦力Ff的关系式进行分析.
解答:当加速度较小时,摩擦力Ff沿斜面向上.将加速度分解为沿斜面向下和垂直于斜面向上.根据牛顿第二定律得
FN-mgcosθ=masinθ,
mgsinθ-Ff=macosθ,
得到FN=mgcosθ+masinθ Ff=mgsinθ-macosθ

可知当a增大时,FN增大,Ff减小.
当加速度较大时,摩擦力Ff沿斜面向下.根据牛顿第二定律得
FN-mgcosθ=masinθ,
mgsinθ+Ff=macosθ,
得到FN-mgcosθ=masinθ,Ff=macosθ-mgsinθ
可知当a增大时,FN增大,Ff增大.故C正确.
故选C
点评:本题考查灵活运用正交分解处理物理问题的能力,采用的是分解加速度,不分解要求的力的方法,使解题过程简洁方便.

练习册系列答案
相关题目
 (2005?和平区一模)如图所示,有一倾角为30°的光滑斜面,斜面长l为10m,一小球从斜面顶端以10m/s的速度沿水平方向抛出,求:
(2005?和平区一模)如图所示,有一倾角为30°的光滑斜面,斜面长l为10m,一小球从斜面顶端以10m/s的速度沿水平方向抛出,求: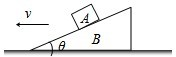 如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( )
如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( ) 如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( )
如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( ) 如图所示,有一倾角为30°的光滑斜面,匀强磁场垂直斜面,匀强电场沿斜面向上并垂直斜面底边.一质量为m、带电荷量为q的小球,以速度v在斜面上做半径为R匀速圆周运动.则( )
如图所示,有一倾角为30°的光滑斜面,匀强磁场垂直斜面,匀强电场沿斜面向上并垂直斜面底边.一质量为m、带电荷量为q的小球,以速度v在斜面上做半径为R匀速圆周运动.则( ) (2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数
(2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数