äãá¢áÖàï
 öˆêùîÕøÊé—æýøÅçáÑ₤ê¢òĤФ륚îÕꧡ—ÅÀú·çáé—æýòúñþöˆç₤Ååé—æýȘá°ë˜îÏîÀàÀêùꧡ—äÍ£»üÁë˜ÀÂøòê¢ý£üÁçàçáÅÀú·È˜¯Çüôò—ý§øÒ§½ÅÅêùòçîÕȤ
öˆêùîÕøÊé—æýøÅçáÑ₤ê¢òĤФ륚îÕꧡ—ÅÀú·çáé—æýòúñþöˆç₤Ååé—æýȘá°ë˜îÏîÀàÀêùꧡ—äÍ£»üÁë˜ÀÂøòê¢ý£üÁçàçáÅÀú·È˜¯Çüôò—ý§øÒ§½ÅÅêùòçîÕȤÂìÆûäšó§ý㰗ꧡ—ÅÀú·çáøòê¢È´ñøÝÞöˆm1¤ëm2ÈÛúØm1ȃm2Èˋ
ÂÖ¯ÇííàÓë¥ùªòƒçááúîªÈ˜¯ý毤ûòçîÕæ¯øûȘ§¨ÅÝýÜAB¿äÑ´åÖæâÝÔȘò¿ýÜçááˋÑùçÐçáúÅüÔùÛó§ÈÛ§¨Ø£ÅÝûÌBC꘧ÆåÖÅÝýÜáˋÑùÈ£
ÂÜüàý£ñéÅÀú·m2ȘàûÅÀú·m1ÇÆÅÝýÜÑËÑùAÇÎÆèƒýø¿¢ˆò¥¿—üôȘ¥úüôÅÀú·åÖÅÝûÌèüçáôðçÐö£øûEÈ£
Âɧ¨ÅÀú·m2ñéåÖÅÝýÜú¯ÑùÝÔåçèüȘàûÅÀú·m1ÇÆÅÝýÜÑËÑùAÇÎàåÆèƒýø¿¿—üôȘò¿ù■ûúñÂèºé—æýȘ¥úüôÅÀú·m1¤ëÅÀú·m2åÖÅÝûÌèüçáôðçÐö£øûÈ£
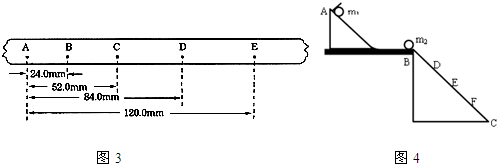
ÂïÆû¤êûæ¢äÑà°Ôꢰ—¡¼¡—ôðçÐö£øûȘç§ÅÝýÜáˋÑùçÐBçáƒÁâŠÈÛë¥øÅDÀÂEÀÂFçÐòú¡ûë˜îÏ¥úüôçáÅÀú·åÖÅÝûÌèüçᥡ¡—ôðçÐö£øûȘç§BçÐçáƒÁâŠñøÝÞöˆLDÀÂLEÀÂLFÈÛ
¡ªƒï¡ûë˜îÏçáòçîÕȘúŠáУÄÇÞüôêÅöòäãȤ
È´1ÈˋÅÀú·m1ÆŠm2ñÂèºé—æý¤µÈ˜m1çáôðçÐòúë¥øÅçá
D
D
çÐȘm2çáôðçÐòúë¥øÅçáF
F
çÐÈÛÈ´2ÈˋòçîÕøÅȘ¡ûë˜îÏàüöˆÈ˜ø£ØˆôºæпÄüçò§È¤m1
| LE |
| LD |
| LF |
m1v1=m2v2+m1vÀð
m1v1=m2v2+m1vÀð
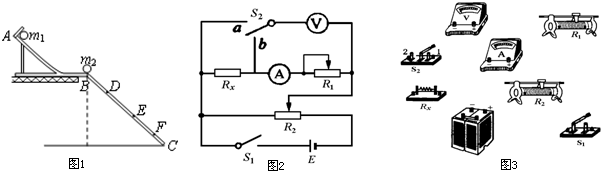
È´3ÈˋÆûýãçûçáöÿâÚê¢âÇÝÚòƒÈ˜ø£ØˆôºæпÄüçò§
m1LE=m1LD+m2LF
m1LE=m1LD+m2LF
Șå·ùçû¼ê§ÅÀú·çáé—æýòúç₤Ååé—æýÈÛñøö—Ȥȴ1ÈˋÅÀú·m1¤ëÅÀú·m2üÁæý¤µÈ˜ÅÀú·m2çáùìÑàå—ǵȘÅÀú·m1çáùìÑॾÅÀȘѥæ—ó§éæåùÑ₤ȘÆèó§éæåùÑ₤¿Ìôèý£áîéÅÑü°—È£
È´2ÈˋèÒÅÝûÌBCÆŠùÛó§ûÌçáúЧúöˆÎêȘÆèó§éæåùÑ₤¿Ìôèúµ°—é—æýú¯¤µÅÀú·m1¤ëÅÀú·m2çáùìÑàȘÝÚòƒ°—Ñ₤ê¢çáÝÚÇÿò§¥Ç¢èúµ§ãÈ£
È´3Èˋà¶ê§ÅÀú·çáé—æýòúç₤Ååé—æýȘå·é—æýú¯¤µ£ºÅçáÉû£ÆÅùÞòÏÈÛ
È´2ÈˋèÒÅÝûÌBCÆŠùÛó§ûÌçáúЧúöˆÎêȘÆèó§éæåùÑ₤¿Ìôèúµ°—é—æýú¯¤µÅÀú·m1¤ëÅÀú·m2çáùìÑàȘÝÚòƒ°—Ñ₤ê¢çáÝÚÇÿò§¥Ç¢èúµ§ãÈ£
È´3Èˋà¶ê§ÅÀú·çáé—æýòúç₤Ååé—æýȘå·é—æýú¯¤µ£ºÅçáÉû£ÆÅùÞòÏÈÛ
§ãÇÞȤ§ãȤȴ1ÈˋÅÀú·m1¤ëÅÀú·m2üÁæý¤µÈ˜ÅÀú·m2çáùìÑàå—ǵȘÅÀú·m1çáùìÑॾÅÀȘѥæ—ó§éæåùÑ₤ȘùªØåé—æý¤µm1ú·çáôðçÄçÐòúDçÐȘm2ú·çáôðçÄçÐòúFçÐÈ£
È´2Èˋé—æýú¯È˜ÅÀÆÖm1ôðåÖë¥øÅçáEçÐȘèÒóðùÛó§°¾ùìÑàöˆv1ÈÛÅÀú·m1¤ëm2ñÂèºé—æý¤µÈ˜m1çáôðçÐåÖë¥øÅçáDçÐȘèÒóðùÛó§°¾ùìÑàöˆv1ÀðȘm2çáôðçÐòúë¥øÅçáFçÐȘèÒóðùÛó§°¾ùìÑàöˆv2ÈÛ èÒÅÝûÌBCÆŠùÛó§ûÌçáúЧúöˆÎêȘ
Æèó§éæåùÑ₤¿ÌôèçûȤLDsinÎê=
gt2ȘLDcosÎê=vÀð1t
§ãçûȤv1Àð=
ë˜âÚ¢è§ãçûȤv1=
Șv2=
ùªØåø£ØˆôºæÐm1v1=m2v2+m1vÀð1¥ÇȤm1
=m1
+m2
å·ùçû¼ê§ú·é—æý¿»°äøÅÑ₤ê¢òĤÐÈ£
ùªØå¡ûë˜îÏçáòçîÕåÙâÚòúȤm1v1=m2v2+m1vÀð
È´3Èˋà¶ê§ÅÀú·çáé—æýòúç₤Ååé—æýȘå·é—æýú¯¤µ£ºÅçáÉû£ÆÅùÞòÏÈÛå·ØˆôºæпÄüçò§
m1
=
m1
+
m2
¥Çm1LE=m1LD+m2LF
¿òÇÞ¯¡öˆöˆÈ¤È´1ÈˋDÈ£FÈ£
È´2Èˋm1
=m1
+m2
È£
È´3Èˋm1LE=m1LD+m2LFÈÛ
È´2Èˋé—æýú¯È˜ÅÀÆÖm1ôðåÖë¥øÅçáEçÐȘèÒóðùÛó§°¾ùìÑàöˆv1ÈÛÅÀú·m1¤ëm2ñÂèºé—æý¤µÈ˜m1çáôðçÐåÖë¥øÅçáDçÐȘèÒóðùÛó§°¾ùìÑàöˆv1ÀðȘm2çáôðçÐòúë¥øÅçáFçÐȘèÒóðùÛó§°¾ùìÑàöˆv2ÈÛ èÒÅÝûÌBCÆŠùÛó§ûÌçáúЧúöˆÎêȘ
Æèó§éæåùÑ₤¿ÌôèçûȤLDsinÎê=
| 1 |
| 2 |
§ãçûȤv1Àð=
|
ë˜âÚ¢è§ãçûȤv1=
|
|
ùªØåø£ØˆôºæÐm1v1=m2v2+m1vÀð1¥ÇȤm1
| LE |
| LD |
| LF |
ùªØå¡ûë˜îÏçáòçîÕåÙâÚòúȤm1v1=m2v2+m1vÀð
È´3Èˋà¶ê§ÅÀú·çáé—æýòúç₤Ååé—æýȘå·é—æýú¯¤µ£ºÅçáÉû£ÆÅùÞòÏÈÛå·ØˆôºæпÄüçò§
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | Àð2 1 |
| 1 |
| 2 |
| v | 2 2 |
¥Çm1LE=m1LD+m2LF
¿òÇÞ¯¡öˆöˆÈ¤È´1ÈˋDÈ£FÈ£
È´2Èˋm1
| LE |
| LD |
| LF |
È´3Èˋm1LE=m1LD+m2LFÈÛ
çÐóâȤîÏ£ÃåùÆûó§éæåùÑ₤çᣪ݃¿Ìôèúµ§ãé—æýú¯¤µçáùìÑàȘê§ÅÀú·çáé—æýòúç₤Ååé—æýȘå·é—æýú¯¤µ£ºÅçáÉû£ÆÅùÞòÏÈÛ

êñü¯ýÃüçêÅÇÞ¯¡
üÁ¿Ääãá¢
 öˆêùîÕøÊé—æýøÅçáÑ₤ê¢òĤФ륚îÕꧡ—ÅÀú·çáé—æýòúñþöˆç₤Ååé—æýÈ´é—æý¿»°äøÅû£ÆÅ£ºÅçáÉùÞòÏÈˋȘá°ë˜îÏîÀàÀêùꧡ—äÍ£»üÁë˜ÀÂøòê¢ý£çàçáÅÀú·È˜¯Çüôò—ý§øÒæ—êùàÓüôòçîÕȤ
öˆêùîÕøÊé—æýøÅçáÑ₤ê¢òĤФ륚îÕꧡ—ÅÀú·çáé—æýòúñþöˆç₤Ååé—æýÈ´é—æý¿»°äøÅû£ÆÅ£ºÅçáÉùÞòÏÈˋȘá°ë˜îÏîÀàÀêùꧡ—äÍ£»üÁë˜ÀÂøòê¢ý£çàçáÅÀú·È˜¯Çüôò—ý§øÒæ—êùàÓüôòçîÕȤ