题目内容
19. 如图所示,在竖直放置的半径为R的光滑绝缘细管的圆心O处放一点电荷,将质量m,带电量为+q的小球从圆弧管的水平直径端点A由静止释放,小球沿细管滑到最低点B时,对管壁恰好无压力,则放于圆心处的电荷带负电,带电量Q=$\frac{{3mgR}^{2}}{kq}$.
如图所示,在竖直放置的半径为R的光滑绝缘细管的圆心O处放一点电荷,将质量m,带电量为+q的小球从圆弧管的水平直径端点A由静止释放,小球沿细管滑到最低点B时,对管壁恰好无压力,则放于圆心处的电荷带负电,带电量Q=$\frac{{3mgR}^{2}}{kq}$.
分析 小球沿细管滑到最低点B过程中,只有重力做功,小球的机械能守恒.小球到达B点时对管壁恰好无压力,则由重力和静电力的合力提供向心力,根据机械能守恒定律求出小球到达B点时的速度,由牛顿第二定律求出静电力的大小,由库仑定律求得电量Q.
解答 解:小球到达B点时对管壁恰好无压力,则由重力和静电力的合力提供向心力,故静电力必定为引力,两电荷的电性相反,故放于圆心处的电荷带负电;
由牛顿第二定律得,F-mg=$\frac{{mv}^{2}}{R}$①
F=$\frac{kQq}{{R}^{2}}$②
从释放到最低点,由动能定理得,mgR=$\frac{1}{2}$mv2③
联立①②③得,Q=$\frac{{3mgR}^{2}}{kq}$
故答案为:负;$\frac{{3mgR}^{2}}{kq}$.
点评 本题是机械能守恒定律和牛顿第二定律的综合应用.对于圆周运动,常常不单独出题,会和动能定理、机械能守恒结合应用

练习册系列答案
相关题目
10.一矩形线圈在匀强磁场中绕一固定转轴作匀速转动,当线圈刚好处于如图所示的位置时,则它的( )


| A. | 磁通量最大,磁通量的变化率最小,感应电动势最小 | |
| B. | 磁通量最大,磁通量的变化率最大,感应电动势最大 | |
| C. | 磁通量为零,磁通量的变化率最大,感应电动势最大 | |
| D. | 磁通量为零,磁通量的变化率最小,感应电动势最小 |
7.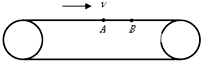 如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )
如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )
 如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )
如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )| A. | 两物体的加速度相同 | |
| B. | 传送带对两物体做功相等 | |
| C. | 乙在传送带上滑行系统产生的热量与甲在传送带上滑行系统产生的热量相等 | |
| D. | 传送带克服摩擦力做的功相等 |
14. 电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )
电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )
 电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )
电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )| A. | 如果v0不同,该战士落到雪坡时的位置不同,速度方向相同 | |
| B. | 如果v0不同,该战士落到雪坡时的位置不同,但空中运动时间相同 | |
| C. | 该战士刚要落到雪坡上时的速度大小是$\frac{{v}_{0}}{cosθ}$ | |
| D. | 该战士在空中经历的时间是$\frac{{v}_{0}tanθ}{g}$ |
4.下列说法正确的是( )
| A. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是轻核聚变 | |
| B. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{54}^{140}$Xe+${\;}_{38}^{94}$Sr+2${\;}_{0}^{1}$n是重核裂变 | |
| C. | ${\;}_{88}^{226}$Ra→${\;}_{86}^{222}$Rn+${\;}_{2}^{4}$He是α衰变 | |
| D. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+${\;}_{-1}^{0}$e是核裂变 |
11. 如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的同定轴转动.开始时OB与地面相垂直,放手后支架开始运动,在不计任何阻力的情况下,下列说法中正确的是( )
如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的同定轴转动.开始时OB与地面相垂直,放手后支架开始运动,在不计任何阻力的情况下,下列说法中正确的是( )
 如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的同定轴转动.开始时OB与地面相垂直,放手后支架开始运动,在不计任何阻力的情况下,下列说法中正确的是( )
如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的同定轴转动.开始时OB与地面相垂直,放手后支架开始运动,在不计任何阻力的情况下,下列说法中正确的是( )| A. | A球到达最低点时速度为零 | |
| B. | A球机械能减少,B球机械能守恒 | |
| C. | B球向左摆动所能达到的最高位置等于A球开始运动时的高度 | |
| D. | 当支架从左向右返回摆动时,A球一定能回到起始高度 |
8.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步.下列表述正确的是( )
| A. | 牛顿通过实验精确测定了引力常量 | |
| B. | 牛顿最终给出了在科学上具有划时代意义的万有引力定律 | |
| C. | 牛顿建立的经典力学适用于宏观、高速、强引力场 | |
| D. | 牛顿建立了狭义相对论,把物理学推进到高速领域 |
9.下列所述的实例中(均不计空气阻力),机械能守恒的是( )
| A. | 小石块被竖直向上抛出后在空中运动的过程 | |
| B. | 木箱沿粗糙斜面匀速下滑的过程 | |
| C. | 人乘电梯匀速上升的过程 | |
| D. | 子弹射穿木块的过程 |
