题目内容
如图所示,ABCD为竖直放在场强为E=104
V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与半圆环相切,A为水平轨道上的一点,而且AB的长度=R=0.2 m.把一质量m=0.1 kg、带电量q=10-4 C的带正电小球,放在水平轨道的A点由静止开始释放后,在轨道的内侧运动.(g取10 m/s2)求:
1.它到达C点时的速度是多大?
2.它到达C点时对轨道压力是多大?
3.若让小球安全通过D点,开始释放点离B点至少多远?
【答案】
1.2 m/s
2.3 N
3.至少0.5m
【解析】(1)由A点到C点应用动能定理
有Eq(AB+R)-mgR=mvC2① (3分)
解得vC=2 m/s. ② (2分)
(2)在C点应用牛顿第二定律得:
FN-Eq=m③ (3分)
解得FN=3 N. ④ (2分)
由牛顿第三定律知,
小球在C点对轨道的压力为3 N. ⑤ (1分)
(3)在D点,小球要安全通过必有
mg≤m⑥ (2分)
设释放点距B点的距离为x m,由动能定理得:
Eqx-mg2R=mvD2⑦ (2分)
以上两式联立可得x≥0.5 m.⑧
即至少0.5m (1分)

练习册系列答案
相关题目
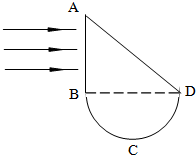 如图所示,ABCD为同种材料构成的柱形透明体的横截面,其中ABD部分为等腰直角三角形,BCD部分为半圆形,一束单色平行光从真空射向AB或AD面,材料折射率n=1.6,下列说法正确的是( )
如图所示,ABCD为同种材料构成的柱形透明体的横截面,其中ABD部分为等腰直角三角形,BCD部分为半圆形,一束单色平行光从真空射向AB或AD面,材料折射率n=1.6,下列说法正确的是( )| A、从AB面中点射入的光线一定从圆弧的中点射出 | B、从AB面射入的所有光线经一次反射和折射后都从BCD面射出 | C、从AB面中间附近射入的所有光线经一次反射和折射后都从BCD面射出 | D、若光线只从AD面垂直射入,则一定没有光线从BCD面射出 |
 如图所示,ABCD为一倾角θ=30°的粗糙斜面,AD边与BC边平行,有一重力G=10N放在斜面上,当对物体施加一个与AB边平行的拉力F时,物体恰能做匀速直线运动.已知物体与斜面的动摩擦因数μ=
如图所示,ABCD为一倾角θ=30°的粗糙斜面,AD边与BC边平行,有一重力G=10N放在斜面上,当对物体施加一个与AB边平行的拉力F时,物体恰能做匀速直线运动.已知物体与斜面的动摩擦因数μ= 如图所示,abcd为质量M=2㎏的导轨,放在光滑绝缘的水平面上,另有一根质量m=0.6㎏的金属棒PQ平行bc放在水平导轨上,PQ棒左边靠着绝缘的竖直立柱e、f,导轨处于匀强磁场中,场以00′为界,左侧的磁场方向竖直向上,右侧的磁场方向水平向右,磁感强度都为B=0.8T.导轨的bc段长L=0.5m,其电阻r=0.4Ω,金属棒的电阻R=0.2Ω,其余电阻均可不计,金属棒与导轨间的动摩擦因数为0.2.若导轨上作用一个方向向左、大小为F=2N的水平拉力,设导轨足够长,g取10m/s2.试求:
如图所示,abcd为质量M=2㎏的导轨,放在光滑绝缘的水平面上,另有一根质量m=0.6㎏的金属棒PQ平行bc放在水平导轨上,PQ棒左边靠着绝缘的竖直立柱e、f,导轨处于匀强磁场中,场以00′为界,左侧的磁场方向竖直向上,右侧的磁场方向水平向右,磁感强度都为B=0.8T.导轨的bc段长L=0.5m,其电阻r=0.4Ω,金属棒的电阻R=0.2Ω,其余电阻均可不计,金属棒与导轨间的动摩擦因数为0.2.若导轨上作用一个方向向左、大小为F=2N的水平拉力,设导轨足够长,g取10m/s2.试求: 如图所示,ABCD为一直角梯形棱镜的截面,∠C=60°P为垂直于直线BC的光屏,现用一宽度等于AB边的单色平行光束垂直射向AB面,经棱镜折射后在屏P上形成宽度等于
如图所示,ABCD为一直角梯形棱镜的截面,∠C=60°P为垂直于直线BC的光屏,现用一宽度等于AB边的单色平行光束垂直射向AB面,经棱镜折射后在屏P上形成宽度等于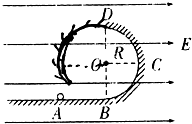 如图所示,ABCD为竖直放在场强为E=104V/m水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的圆形轨道,轨道的水平部分与其半圆相切,A为水平轨道上的一点,而且AB=R=0.2m,把一质量m=0.1kg、带电荷量q=+1×10-4C的小球放在水平轨道的A点由静止开始释放,小球在轨道的内侧运动.(g取10m/s2)求:
如图所示,ABCD为竖直放在场强为E=104V/m水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的圆形轨道,轨道的水平部分与其半圆相切,A为水平轨道上的一点,而且AB=R=0.2m,把一质量m=0.1kg、带电荷量q=+1×10-4C的小球放在水平轨道的A点由静止开始释放,小球在轨道的内侧运动.(g取10m/s2)求: