题目内容
如图所示,A、B质量分别为ml=1㎏,m2=2kg,置于小车C上,小车质量m3=1kg,A、B间粘有少量炸药,A、B与小车间的动摩擦因数均为0.5,小车静止在光滑水平上,菲炸药爆炸释放的能量有12J转化为A、B的机械能,其余的转化为内能,A、B始终在小车表面水平运动,求:(1)A、B开始运动的初速度;
(2)A、B在小车上滑行的时间.

【答案】分析:物体A、B系统所受外力的合力为零,系统动量守恒;根据动量守恒定律和能量守恒定律列式后联立求解即可.
解答:解:(1)炸药爆炸瞬间A、B系统动量守恒,以向右为正方向,有:
0=m1v1+m2v2
A、B的机械能总量为12J,故:
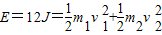
联立解得:
得v1=4m/s v2=-2m/s
或者v1=-4m/s v2=+2m/s(不合实际,舍去)
(2)爆炸后AB在C上滑动,B先与C相对静止,设此时A的速度为v3,B、C的速度为v4,该过程中ABC组成的系统动量守恒.
设该过程的时间为t3,对A应用动量定理:-μm1gt3=m1v3-m1v1
对B应用动量定理:-μm2gt3=m2v4-m2v2
对C应用动量定理:(μm2g-μm1g)t3=m3v4
代人数据得:v3=3m/s;v4=-1m/s;t3=0.2s
之后,A在C是滑动直到相对静止,根据系统的动量守恒,
0=(m1+m2+m3)v
解得:v=0
设A滑动的总时间为t,则:-μm1gt=0-m1v1
解得:t=0.8s
答:(1)A爆炸后获得的速度的大小为4m/s;B爆炸后获得的速度的大小为2m/s
(2)A在小车上滑行的时间为0.8s,B在小车上滑行的时间为0.2s.
点评:本题关键是明确爆炸过程系统动量守恒,同时结合能量守恒定律、动量定理和能量的转化与守恒列式求解,中档题.
解答:解:(1)炸药爆炸瞬间A、B系统动量守恒,以向右为正方向,有:
0=m1v1+m2v2
A、B的机械能总量为12J,故:
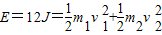
联立解得:
得v1=4m/s v2=-2m/s
或者v1=-4m/s v2=+2m/s(不合实际,舍去)
(2)爆炸后AB在C上滑动,B先与C相对静止,设此时A的速度为v3,B、C的速度为v4,该过程中ABC组成的系统动量守恒.
设该过程的时间为t3,对A应用动量定理:-μm1gt3=m1v3-m1v1
对B应用动量定理:-μm2gt3=m2v4-m2v2
对C应用动量定理:(μm2g-μm1g)t3=m3v4
代人数据得:v3=3m/s;v4=-1m/s;t3=0.2s
之后,A在C是滑动直到相对静止,根据系统的动量守恒,
0=(m1+m2+m3)v
解得:v=0
设A滑动的总时间为t,则:-μm1gt=0-m1v1
解得:t=0.8s
答:(1)A爆炸后获得的速度的大小为4m/s;B爆炸后获得的速度的大小为2m/s
(2)A在小车上滑行的时间为0.8s,B在小车上滑行的时间为0.2s.
点评:本题关键是明确爆炸过程系统动量守恒,同时结合能量守恒定律、动量定理和能量的转化与守恒列式求解,中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,A.B质量分别为mA=1kg,mB=2kg,A与小车壁的动摩擦因数为0.5,B与小车间的摩擦不计,要使B与小车保持相对静止,求小车的加速度应为多大?(设最大静摩擦力等于滑动摩擦力)
如图所示,A.B质量分别为mA=1kg,mB=2kg,A与小车壁的动摩擦因数为0.5,B与小车间的摩擦不计,要使B与小车保持相对静止,求小车的加速度应为多大?(设最大静摩擦力等于滑动摩擦力) 一颗子弹,质量为m,以初速度v0向右先后击穿放在光滑水平面上靠在一起的A、B两完全相同物体,如图所示,A、B质量均为M,子弹在A、B中所受阻力恒为f,在A内穿行时间为t1,在B内穿行时间为t2,求子弹在A内穿行期间A、B间相互作用力的大小及B的最终速度.
一颗子弹,质量为m,以初速度v0向右先后击穿放在光滑水平面上靠在一起的A、B两完全相同物体,如图所示,A、B质量均为M,子弹在A、B中所受阻力恒为f,在A内穿行时间为t1,在B内穿行时间为t2,求子弹在A内穿行期间A、B间相互作用力的大小及B的最终速度. 如图所示,A、B质量分别为mA和mB,叠放在倾角为θ的斜面上以相同的速度匀速下滑,则( )
如图所示,A、B质量分别为mA和mB,叠放在倾角为θ的斜面上以相同的速度匀速下滑,则( )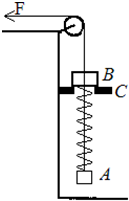 如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用轻质弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求:
如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用轻质弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求: