题目内容
16.如图甲所示,固定于水平桌面上的金属导轨abcd足够长,质量为20kg的金属棒ef搁在导轨上,可无摩擦地滑动,此时bcfe构成一个边长为L=1m的正方形.金属棒的电阻为r=1Ω,其余部分的电阻不计.在t=0的时刻,导轨间加一竖直向下的磁场,磁感应强度随时间的变化如图乙所示,其中B1=10T,t1=1s.为使金属棒ef在0~t1保持静止,;需在金属棒ef上施加一水平拉力F,从t1时刻起保持此时的水平拉力F不变,金属棒ef在导轨上运动了距离s=1m时,刚好达到最大速度,求:
(1)在t=0.5s时刻,流过金属棒的电流方向以及该水平拉力F的大小和方向;
(2)金属棒ef在导轨上运动的最大速度;
(3)从t=0开始到金属棒ef达到最大速度的过程中,金属棒ef中产生的热量.
分析 (1)由法拉第电磁感应定律求出感应电动势,由F=BIL求出安培力,由楞次定律判断出感应电流的方向,由左手定则判断出安培力的方向,由平衡条件求出拉力大小与方向;
(2)当拉力与安培力相等时,导体棒做匀速运动,速度达到最大,求出拉力,根据安培力公式求出导体棒的最大速度;
(3)由焦耳定律求出导体棒静止时产生的焦耳热,由能量守恒定律求出导体棒运动时产生的焦耳热,然后求出整个过程产生的焦耳热.
解答 解:(1)在t=0.5s时刻,由楞次定律可知,电流方向从f到e
感应电动势 E=$\frac{△B}{△t}$S=$\frac{{B}_{1}{L}^{2}}{{t}_{1}}$=10V
感应电流 I=$\frac{E}{r}$=10A
导体棒受到的安培力 F安=$\frac{{B}_{1}}{2}$•I•L=50N,方向水平向左.
(2)当金属棒的速度最大时
感应电动势E′=B1Lvm,
此时导体棒受到的安培力 F安′=B1•I1•L=B1$\frac{{B}_{1}L{v}_{m}}{r}$L=$\frac{{B}_{1}^{2}{L}^{2}{v}_{m}}{r}$
此时拉力 F′=B1•I•L=100N
当金属棒的速度最大时 F′=F安′
所以vm=1m/s
(3)金属棒静止时I1=10A,Q1=${I}_{1}^{2}r{t}_{1}$=100J
金属棒从开始运动到最大速度阶段由能量守恒得
Q2=F′s-$\frac{1}{2}m{v}_{m}^{2}$=90J
所以,全过程产生的焦耳热 Q=Q1+Q2=190J
答:
(1)在t=0.5s时刻,流过金属棒的电流方向从f到e,该水平拉力F的大小为50N,方向水平向左;
(2)金属棒ef在导轨上运动的最大速度是1m/s;
(3)从t=0开始到金属棒ef达到最大速度的过程中,金属棒ef中产生的热量是190J.
点评 导体棒静止时,磁感应强度均匀变化,产生的感应电动势是定值,感应电流是定值,但导体棒受到的安培力F=BIL是变力;导体棒在拉力作用下向右运动时,做的是加速度逐渐减小的加速运动,最后做匀速直线运动,对导体棒正确受力分析,分析清楚导体棒的运动过程是正确解题的关键.

 如图所示,用一长为l=0.5m的轻杆拴接一质量为m=0.1kg的小球在竖直面内做圆周运动,当其运动到最高点时,其速度为v=2m/s,g取10N/kg,则关于杆所受到的力,下列说法中正确的是( )
如图所示,用一长为l=0.5m的轻杆拴接一质量为m=0.1kg的小球在竖直面内做圆周运动,当其运动到最高点时,其速度为v=2m/s,g取10N/kg,则关于杆所受到的力,下列说法中正确的是( )| A. | 杆对物体的作用力为支持力,且大小为0.8N | |
| B. | 杆对物体的作用力为支持力,且大小为0.2N | |
| C. | 杆对物体的作用力为拉力,且大小为0.8N | |
| D. | 杆对物体的作用力为拉力,且大小为0.2N |
 如图所示,空间存在着沿x轴方向的静电场,A、O、B为x轴上的点,图中的折线表示的是一带正电粒子沿x轴在A、B两点间运动时,其电势能EP随x的变化情况.若$\overline{AO}$>$\overline{OB}$,则下列判断正确的是( )
如图所示,空间存在着沿x轴方向的静电场,A、O、B为x轴上的点,图中的折线表示的是一带正电粒子沿x轴在A、B两点间运动时,其电势能EP随x的变化情况.若$\overline{AO}$>$\overline{OB}$,则下列判断正确的是( )| A. | A、B两点的电势一定相等 | |
| B. | 粒子从A向O运动过程中所受电场力均匀增大 | |
| C. | A、O间的电场强度大于O、B间的电场强度 | |
| D. | 若将一带负电的粒子从A点由静止释放,则当粒子运动到O点时动能最大 |
 在静电场中,一个电子只在电场力的作用下,沿着圆弧由A点运动到B点,在这个运动过程中,下列说法过程中正确的是( )
在静电场中,一个电子只在电场力的作用下,沿着圆弧由A点运动到B点,在这个运动过程中,下列说法过程中正确的是( )| A. | 该电子速度大小一定增加 | B. | A点的场强一定比B点的场强大 | ||
| C. | A、B两点的电势一定相等 | D. | 电子的电势能可能增大 |
 一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )
一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )| A. | E1<$\frac{kQ}{4{R}^{2}}$ | |
| B. | E2=$\frac{kQ}{4{R}^{2}}$ | |
| C. | 电荷Q在球心O处产生的场强方向垂直于底面向下 | |
| D. | 电荷Q在球心O处产生的场强方向垂直于底面向上 |
| A. | 在定义加速度,电场强度,电容器的电容等物理量时采用了类比法 | |
| B. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| C. | 在用实验探究加速度、力和质量三者之间关系时,应用了控制变量法 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
 把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )| A. | A端的电势比B端的电势高 | |
| B. | A端的电荷比B端的电荷密集 | |
| C. | A端额电势可能比B端的电势高,也可能比B端的电势低 | |
| D. | A端的电势与B端的电势相等 |
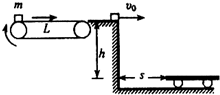 如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求:
如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求: