题目内容
如图,板长为L的平行板电容器倾斜固定放置,极板与水平线夹角θ=30°,某时刻一质量为m,带电量为q的小球由正中央A点静止释放,小球离开电场时速度是水平的,落到距离A点高度为h的水平面处的B点,B点放置一绝缘弹性平板M,当平板与水平夹角α=45°时,小球恰好沿原路返回A点.求:

(1)电容器极板间的电场强度;
(2)平板电容器的板长L;
(3)球在AB间运动的周期.

(1)电容器极板间的电场强度;
(2)平板电容器的板长L;
(3)球在AB间运动的周期.
分析:(1)由于带电粒子做的直线运动,对带电粒子受力分析可知,粒子在电场中的受到的合力沿水平方向,在竖直方向上受力平衡,由此可以求得电场强度的大小;
(2)粒子离开电场后做的是平抛运动,水平方向的速度即为在电场中加速获得的速度的大小,再根据动能定理可以求得极板的长度;
(3)小球在AB间运动的周期即为在电场中加速的时间和平抛运动时间的和.
(2)粒子离开电场后做的是平抛运动,水平方向的速度即为在电场中加速获得的速度的大小,再根据动能定理可以求得极板的长度;
(3)小球在AB间运动的周期即为在电场中加速的时间和平抛运动时间的和.
解答:解:(1)带电粒子沿水平方向做匀加速运动可知:Eqcosθ=mg,
得:E=
=
(2)小球垂直落到弹性挡板上,且α=450,有:v0=vy=
根据动能定理:Eq?
Ltanθ=
m
得:L=
h
(3)由于小球在复合场中做匀加速运动,有:
=
gtanθ
得:t1=
=
平抛运动的时间为:t2=
总时间为:t=2t1+2t2=2(
+
)
答:(1)电容器极板间的电场强度E为
;
(2)平行板电容器的板长L为
h;
(3)小球在AB间运动的周期T为2(
+
).
得:E=
| mg |
| qcosθ |
2
| ||
| 3q |
(2)小球垂直落到弹性挡板上,且α=450,有:v0=vy=
| 2gh |
根据动能定理:Eq?
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
得:L=
| 4 |
| 3 |
(3)由于小球在复合场中做匀加速运动,有:
| L |
| 2cosθ |
| 1 |
| 2 |
| t | 2 1 |
得:t1=
|
|
平抛运动的时间为:t2=
|
总时间为:t=2t1+2t2=2(
|
|
答:(1)电容器极板间的电场强度E为
2
| ||
| 3q |
(2)平行板电容器的板长L为
| 4 |
| 3 |
(3)小球在AB间运动的周期T为2(
|
|
点评:在题目中告诉粒子在电场中做直线运动,由此可以得出,粒子在电场中做的应该是匀加速直线运动,这是本题中的关键所在.

练习册系列答案
相关题目
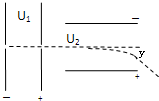 如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后垂直射入电势差为U2的两板距离为d,板长为L的平行极板间的电场中,整个装置处于真空中,重力可忽略,在满足电子能射出平行板区的条件下,设电子的电量为e,质量为m.求:
如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后垂直射入电势差为U2的两板距离为d,板长为L的平行极板间的电场中,整个装置处于真空中,重力可忽略,在满足电子能射出平行板区的条件下,设电子的电量为e,质量为m.求:

 0沿两板间的中心线射入,射出电场时粒子速度的偏转角为37°。已知sin37°=0.6,cos37°=0.8,不计粒子的重力。
0沿两板间的中心线射入,射出电场时粒子速度的偏转角为37°。已知sin37°=0.6,cos37°=0.8,不计粒子的重力。
 0沿两板间的中心线射入,射出电场时粒子速度的偏转角为37°。已知sin37°=0.6,cos37°=0.8,不计粒子的重力。
0沿两板间的中心线射入,射出电场时粒子速度的偏转角为37°。已知sin37°=0.6,cos37°=0.8,不计粒子的重力。