已知某一随机变量X的概率分布列如下,且E(X)=7,求D(X)= .
| X | a | 5 | 9 |
| P | 0.1 | 0.3 | b |
选修4-2矩阵与变换
(Ⅰ)已知矩阵A=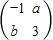 所对应的线性变换把直线l:2x-y=3变换为自身,求A-1.
所对应的线性变换把直线l:2x-y=3变换为自身,求A-1.
(Ⅱ)已知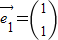 是矩阵B=
是矩阵B=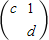 属于特征值λ1=2的一个特征向量,求矩阵B及其另一个特征值及其对应的一个特征向量.
属于特征值λ1=2的一个特征向量,求矩阵B及其另一个特征值及其对应的一个特征向量.
(Ⅰ)已知矩阵A=
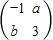 所对应的线性变换把直线l:2x-y=3变换为自身,求A-1.
所对应的线性变换把直线l:2x-y=3变换为自身,求A-1.(Ⅱ)已知
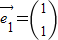 是矩阵B=
是矩阵B=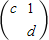 属于特征值λ1=2的一个特征向量,求矩阵B及其另一个特征值及其对应的一个特征向量.
属于特征值λ1=2的一个特征向量,求矩阵B及其另一个特征值及其对应的一个特征向量.
在对人们休闲方式的调查中.现随机抽查了n个人,已知男性占总调查人数的 ,女性占总调查人数的
,女性占总调查人数的 ,其中男性有一半的休闲方式是运动;而女性只有
,其中男性有一半的休闲方式是运动;而女性只有 的休闲方式是运动,经过调查人员的计算:在犯错误的概率不超过0.05的前提下,认为休闲方式与性别有关,那么被调查的人中最少有多少人的休闲方式是运动?
的休闲方式是运动,经过调查人员的计算:在犯错误的概率不超过0.05的前提下,认为休闲方式与性别有关,那么被调查的人中最少有多少人的休闲方式是运动?
参考数据与公式:m=60,其中n=a+b+c+d.
临界值表:
 ,女性占总调查人数的
,女性占总调查人数的 ,其中男性有一半的休闲方式是运动;而女性只有
,其中男性有一半的休闲方式是运动;而女性只有 的休闲方式是运动,经过调查人员的计算:在犯错误的概率不超过0.05的前提下,认为休闲方式与性别有关,那么被调查的人中最少有多少人的休闲方式是运动?
的休闲方式是运动,经过调查人员的计算:在犯错误的概率不超过0.05的前提下,认为休闲方式与性别有关,那么被调查的人中最少有多少人的休闲方式是运动?参考数据与公式:m=60,其中n=a+b+c+d.
临界值表:
| P(K2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
(1)该同学为了求出y关于x的线性回归方程 =
= +
+ ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出 =0.6,试求出
=0.6,试求出 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| y(万盒) | 4 | 4 | 5 | 6 | 6 |
 =
= +
+ ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出 =0.6,试求出
=0.6,试求出 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望.
广东省汕头市日前提出,要提升市民素质和城市文明程度,促进经济发展有大的提速,努力实现“幸福汕头”的共建共享.现随机抽取50位市民,对他们的幸福指数进行统计分析,得到如下分布表:
(I)求这50位市民幸福指数的数学期望(即平均值);
(11)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数.求ξ的分布列;
(III)从这50位市民中,先随机选一个人.记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P.
0 77354 77362 77368 77372 77378 77380 77384 77390 77392 77398 77404 77408 77410 77414 77420 77422 77428 77432 77434 77438 77440 77444 77446 77448 77449 77450 77452 77453 77454 77456 77458 77462 77464 77468 77470 77474 77480 77482 77488 77492 77494 77498 77504 77510 77512 77518 77522 77524 77530 77534 77540 77548 266669
| 幸福级别 | 非常幸福 | 幸福 | 不知道 | 不幸福 |
| 幸福指数(分) | 90 | 60 | 30 | |
| 人数(个) | 19 | 21 | 7 | 3 |
(11)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数.求ξ的分布列;
(III)从这50位市民中,先随机选一个人.记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P.

 ;现已知等比数列{bn}(bn>0,n∈N*),bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n= .
;现已知等比数列{bn}(bn>0,n∈N*),bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n= .