 为了让学生更多的了解“数学史”知识,某中学高一年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据频率分布表,解答下列问题:
为了让学生更多的了解“数学史”知识,某中学高一年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据频率分布表,解答下列问题:| 序号 (i) | 分组 (分数) | 组中值(Gi) | 频数 (人数) | 频率(Fi) |
| 1 | [60,70) | 65 | ① | 0.16 |
| 2 | [70,80) | 75 | 22 | ② |
| 3 | [80,90) | 85 | 14 | 0.28 |
| 4 | [90,100] | 95 | ③ | ④ |
| 合 计 | 50 | 1 | ||
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于80分的同学能获奖,那么可以估计在参加的800名学生中大概有多少同学获奖?
(3)在上述统计数据的分析中有一项计算见算法流程图,求输出S的值.
某调查者从调查中获知某公司近年来科研费用支出(Xi)与公司所获得利润(Yi)的统计资料如下表:
科研费用支出(Xi)与利润(Yi)统计表 单位:万元
(1)过去6年的科研费用平均支出和平均利润是多少?
(2)试估计利润(Yi)对科研费用支出(Xi)的线性回归模型.
(3)若公司希望在2013年的利润比2012年翻一倍,那么公司在2013年科研费用支出的预算应该为多少?
0 74853 74861 74867 74871 74877 74879 74883 74889 74891 74897 74903 74907 74909 74913 74919 74921 74927 74931 74933 74937 74939 74943 74945 74947 74948 74949 74951 74952 74953 74955 74957 74961 74963 74967 74969 74973 74979 74981 74987 74991 74993 74997 75003 75009 75011 75017 75021 75023 75029 75033 75039 75047 266669
科研费用支出(Xi)与利润(Yi)统计表 单位:万元
| 年份 | 科研费用支出 | 利润 |
| 2007 | 5 | 31 |
| 2008 | 11 | 40 |
| 2009 | 4 | 30 |
| 2010 | 5 | 34 |
| 2011 | 3 | 25 |
| 2012 | 2 | 20 |
| 合计 | 30 | 180 |
(2)试估计利润(Yi)对科研费用支出(Xi)的线性回归模型.
(3)若公司希望在2013年的利润比2012年翻一倍,那么公司在2013年科研费用支出的预算应该为多少?
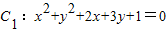 ,圆
,圆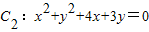 ,则圆C1与圆C2的位置关系是 .
,则圆C1与圆C2的位置关系是 .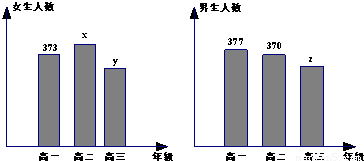
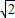 ,
,