为了让学生更多的了解“数学史”知识，某中学高一年级举办了一次“追寻先哲的足迹，倾听数学的声音”的数学史知识竞赛活动，共有800名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据频率分布表，解答下列问题：| 序号 （i） | 分组 （分数） | 组中值（Gi） | 频数 （人数） | 频率（Fi） |
| 1 | [60，70） | 65 | ① | 0.16 |
| 2 | [70，80） | 75 | 22 | ② |
| 3 | [80，90） | 85 | 14 | 0.28 |
| 4 | [90，100] | 95 | ③ | ④ |
| 合 计 | 50 | 1 | ||
（2）为鼓励更多的学生了解“数学史”知识，成绩不低于80分的同学能获奖，那么可以估计在参加的800名学生中大概有多少同学获奖？
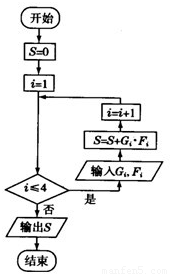
（3）在上述统计数据的分析中有一项计算见算法流程图，求输出S的值．
某调查者从调查中获知某公司近年来科研费用支出（Xi）与公司所获得利润（Yi）的统计资料如下表：
科研费用支出（Xi）与利润（Yi）统计表 单位：万元
（1）过去6年的科研费用平均支出和平均利润是多少？
（2）试估计利润（Yi）对科研费用支出（Xi）的线性回归模型．
（3）若公司希望在2013年的利润比2012年翻一倍，那么公司在2013年科研费用支出的预算应该为多少？
0 74846 74854 74860 74864 74870 74872 74876 74882 74884 74890 74896 74900 74902 74906 74912 74914 74920 74924 74926 74930 74932 74936 74938 74940 74941 74942 74944 74945 74946 74948 74950 74954 74956 74960 74962 74966 74972 74974 74980 74984 74986 74990 74996 75002 75004 75010 75014 75016 75022 75026 75032 75040 266669
科研费用支出（Xi）与利润（Yi）统计表 单位：万元
| 年份 | 科研费用支出 | 利润 |
| 2007 | 5 | 31 |
| 2008 | 11 | 40 |
| 2009 | 4 | 30 |
| 2010 | 5 | 34 |
| 2011 | 3 | 25 |
| 2012 | 2 | 20 |
| 合计 | 30 | 180 |
（2）试估计利润（Yi）对科研费用支出（Xi）的线性回归模型．
（3）若公司希望在2013年的利润比2012年翻一倍，那么公司在2013年科研费用支出的预算应该为多少？
，
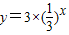的图象，可以把函数
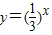的图象（ ）