下列推理:
①由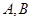 为两个不同的定点,动点
为两个不同的定点,动点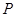 满足
满足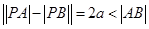 ,得点
,得点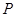 的轨迹为双曲线
的轨迹为双曲线
②由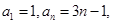 ,求出
,求出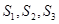 猜想出数列
猜想出数列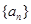 的前
的前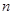 项和
项和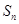 的表达式
的表达式
③由圆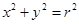 的面积
的面积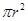 ,猜想出椭圆
,猜想出椭圆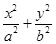 =1的面积
=1的面积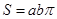
④科学家利用鱼的沉浮原理制造潜艇。其中是归纳推理的命题个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
有一个奇数列1,3,5,7,9,…,现进行如下分组:第1组含有一个数{1},第2组含两个数{3,5};第3组含三个数{7,9,11};…试观察每组内各数之和与其组的编号数n的关系为( ).
| A.等于n2 | B.等于n3 | C.等于n4 | D.等于n(n+1) |
下列说法中正确的是( ).
| A.合情推理就是正确的推理 | B.合情推理就是归纳推理 |
| C.归纳推理是从一般到特殊的推理过程 | D.类比推理是从特殊到特殊的推理过程 |
用数学归纳法证明(n+1)(n+2)(n+3)…(n+n)= (n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
(n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
| A.2k+1 | B.2(2k+1) | C. | D. |
已知a,b,c都是正数,则三数 ( )
( )
| A.都大于2 | B.都小于2 |
| C.至少有一个不大于2 | D.至少有一个不小于2 |
若 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D.由 的取值确定 的取值确定 |
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 |
| B.由a1=a,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆 的面积S=πab 的面积S=πab |
| D.科学家利用鱼的沉浮原理制造潜艇 |
用反证法证明“方程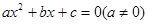 至多有两个解”的假设中,正确的是( )
至多有两个解”的假设中,正确的是( )
| A.至多有一个解 | B.有且只有两个解 |
| C.至少有三个解 | D.至少有两个解 |
利用数学归纳法证明 ,在验证n=1成立时,左边应该是( )
,在验证n=1成立时,左边应该是( )
| A.1 | B. | C. | D. |
有一段演绎推理是这样的:“指数函数 是增函数;
是增函数; 是指数函数;
是指数函数; 是增函数”,结论显然是错误的,原因是( )
是增函数”,结论显然是错误的,原因是( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |