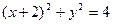如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G。给出下列三个结论:
1AD+AE=AB+BC+CA;
2AF·AG=AD·AE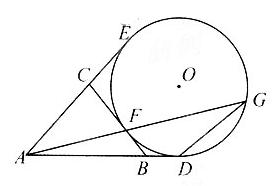
③△AFB ~△ADG
其中正确结论的序号是
| A.①② | B.②③ |
| C.①③ | D.①②③ |
曲线的极坐标方程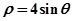 化为直角坐标为( )。
化为直角坐标为( )。
A.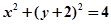 | B.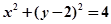 |
C.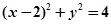 | D.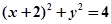 |
曲线的极坐标方程 化为直角坐标为( )。
化为直角坐标为( )。
A. | B. |
C. | D. |
极坐标方程 所表示的图形是
所表示的图形是
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
如图,在直角梯形ABCD中.上底AD= ,下底BC=3
,下底BC=3 ,与两底垂直的腰AB
,与两底垂直的腰AB =6,在AB上选取一点P,使△PA
=6,在AB上选取一点P,使△PA D和△PBC相似,这样的点P( )
D和△PBC相似,这样的点P( )
| A.不存在 | B.有1个 | C.有2个 | D.有3个 |
.点M的球坐标为(8, ,
,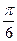 ),则它的直角坐标为( )
),则它的直角坐标为( )
A.(6,4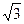 ,2 ,2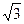 ) ) | B.(6,4,2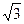 ) ) |
C.(6,2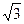 ,4 ,4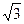 ) ) | D.(6,2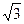 ,4) ,4) |
直角坐标为(-3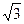 ,3)的点的极坐标可能是( )
,3)的点的极坐标可能是( )
A.(6,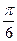 ) ) | B.(-6,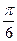 ) ) | C.(6,-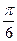 ) ) | D.(-6,-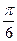 ) ) |
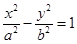 的左焦点F作⊙O:
的左焦点F作⊙O: 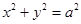 的两条切线,记切点为A,B,双曲线左顶点为C,若
的两条切线,记切点为A,B,双曲线左顶点为C,若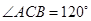 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )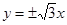
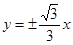
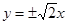
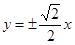
 已知点P的极坐标为(4,
已知点P的极坐标为(4, ),那么过点P且垂直于极轴的直线的极坐标方程是( )
),那么过点P且垂直于极轴的直线的极坐标方程是( )



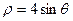 化为直角坐标方程为( )。
化为直角坐标方程为( )。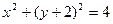 B
B 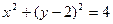
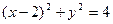 D
D